Giải tích phân lượng giác bằng phương pháp đặt ẩn phụ

Phương pháp đặt ẩn phụ là một trong những phương pháp tối ưu nhất dùng để giải bài toán tích phân lượng giác.

Tích phân hàm lượng giác tổng quát có dạng:

${\displaystyle I={\int }_a^{b}F(\sin x,\cos x)dx}$
Tùy thuộc vào tính chất và dạng đặc biệt của hàm $F(\sin x,\cos x)$ hoăc mối quan hệ giữa hàm $F(\sin x,\cos x)$ với các cận lấy tích phân mà chúng ta sử dụng phép biến đổi tương đương.

DẠNG 1. $F(\sin x,\cos x)=F(-\sin x,-\cos x)$ ($F$ là hàm số chẵn theo $\sin x$ và $\cos x$)

Cách giải: Đặt $t=\tan x$ hoăc $t=\cot x$

Ví dụ 1. Tính tích phân

${\displaystyle I={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{\sqrt[3]{{\sin }^{3}x-\sin x}}{{\sin }^{3}x}\cot xdx}$

Giải:

Rõ ràng $F=\frac{\sqrt[3]{{\sin }^{3}x-\sin x}}{{\sin }^{3}x}\cot x=\frac{\sqrt[3]{(-\sin x{)}^3-(-\sin x)}}{(-\sin x{)}^3}\cdot \frac{-\cos x}{-\sin x}$ nên nó là hàm số chẵn theo $\sin x$ và $\cos x$.

Ta có:

${\displaystyle I={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{\sqrt[3]{1-\frac{1}{{\sin }^{2}x}}}{{\sin }^{2}x}\cot xdx={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{\sqrt[3]{1-\left(1+{\cot }^{2}x\right)}}{{\sin }^{2}x}\cot xdx=-{\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{\sqrt[3]{{\cot }^{2}x}}{{\sin }^{2}x}\cot xdx}$

Đặt $t=\cot x\Rightarrow dt=-\frac{1}{{\sin }^{2}x}dx$

Khi $x=\frac{\pi }{6}\Rightarrow t=\sqrt{3};x=\frac{\pi }{3}\Rightarrow t=\frac{1}{\sqrt{3}}$

Từ đó

${\displaystyle I={\int }_{\sqrt{3}}^{\frac{1}{\sqrt{3}}}{t}^{\frac{1}{3}}\cdot tdt={\int }_{\sqrt{3}}^{\frac{1}{\sqrt{3}}}{t}^{\frac{5}{3}}dt=\sqrt{\frac{1}{8}(9\sqrt[3]{3}-\frac{1}{\sqrt[3]{3}})}}$

DẠNG 2. $F(\sin x,\cos x)=-F(\sin x,-\cos x)$ ($F$ là hàm số lẻ theo $\cos x$)

Cách giải: Đặt $t=\sin x$

Ví dụ 2. Tính tích phân

${\displaystyle I={\int }_0^{\frac{\pi }{2}}\frac{\sin 2x}{(2+\sin x{)}^2}dx}$

Giải:

Ta thấy $F=\frac{\sin 2x}{(2+\sin x{)}^2}=\frac{2\sin x\cos x}{(2+\sin x{)}^2}=-\frac{2\sin x(-\cos x)}{(2+\sin x{)}^2}$ nên $F$ là hàm số lẻ theo $\cos x$
Ta có

${\displaystyle I={\int }_0^{\frac{\pi }{2}}\frac{2\sin x\cos x}{(2+\sin x{)}^2}dx}$

Đặt $t=\sin x\Rightarrow dt=\cos xdx$

Khi $x=0\Rightarrow t=0;x=\frac{\pi }{2}\Rightarrow t=1$

Từ đó:

${\displaystyle I={\int }_0^1\frac{t}{(2+t{)}^2}dt=2({\int }_0^1\frac{1}{2+t}dt-{\int }_0^1\frac{1}{(2+t{)}^2}dt)=2(\ln \frac{3}{2}-\frac{1}{3})}$

DẠNG 3. $F(\sin x,\cos x)=-F(-\sin x,\cos x)$ ($F$ là hàm số lẻ theo $\sin x$)

Cách giải: Đặt $t=\cos x$

Ví dụ 3. Tính tích phân

${\displaystyle I={\int }_0^{\frac{\pi }{6}}\frac{\sin x-{\sin }^{3}x}{\cos 2x}dx}$

Giải:

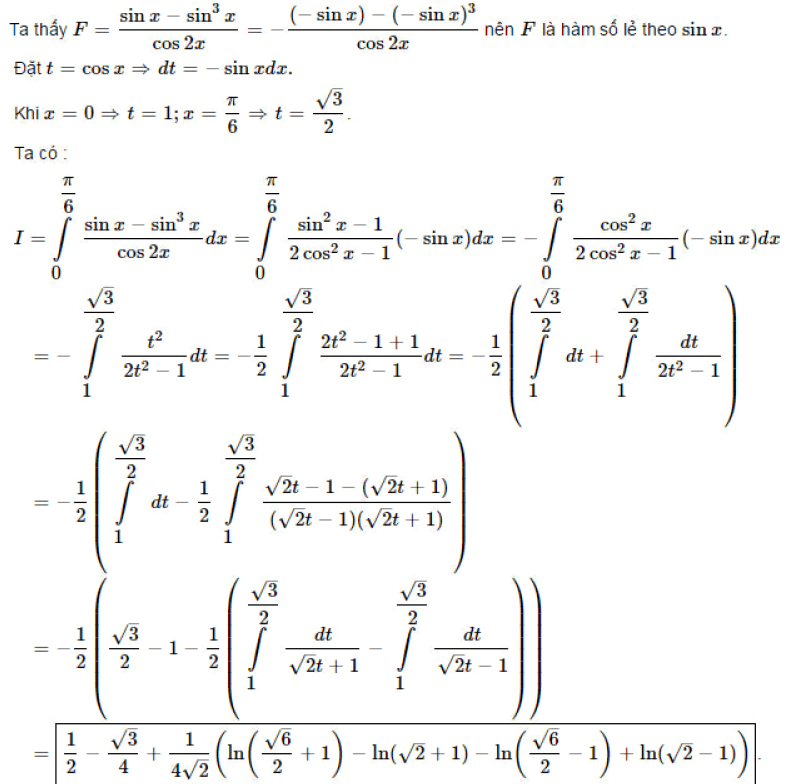
DẠNG 4. $F(\sin x,\cos x)=\frac{a_1\sin x+b_1\cos x+c_1}{a_2\sin x+b_2\cos x+c_2}$

Cách giải: Đặt $t=\tan \frac{x}{2}$

Ví dụ 4. Tính tích phân ${\displaystyle I={\int }_0^{\frac{\pi }{2}}\frac{dx}{4\sin x+3\cos x+5}}$

Giải:

Đặt $t=\tan \frac{x}{2}\Rightarrow \{\begin{array}{l}dx=\frac{2dt}{1+t^2}\\ \sin x=\frac{2t}{1+t^2};\cos x=\frac{1-t^2}{1+t^2}\end{array}$

Khi $x=0\Rightarrow t=1;x=\frac{\pi }{2}\Rightarrow t=1$

Ta có

${\displaystyle I={\int }_0^1\frac{1}{\frac{8t}{1+t^2}+3\frac{1-t^2}{1+t^2}+5}\cdot \frac{2dt}{1+t^2}={\int }_0^1\frac{dt}{t^2+4t+4}={\int }_0^1\frac{d(t+2)}{(t+2{)}^2}=\frac{1}{6}}$

Một số bài toán tích tích phân lượng giác có lời giải

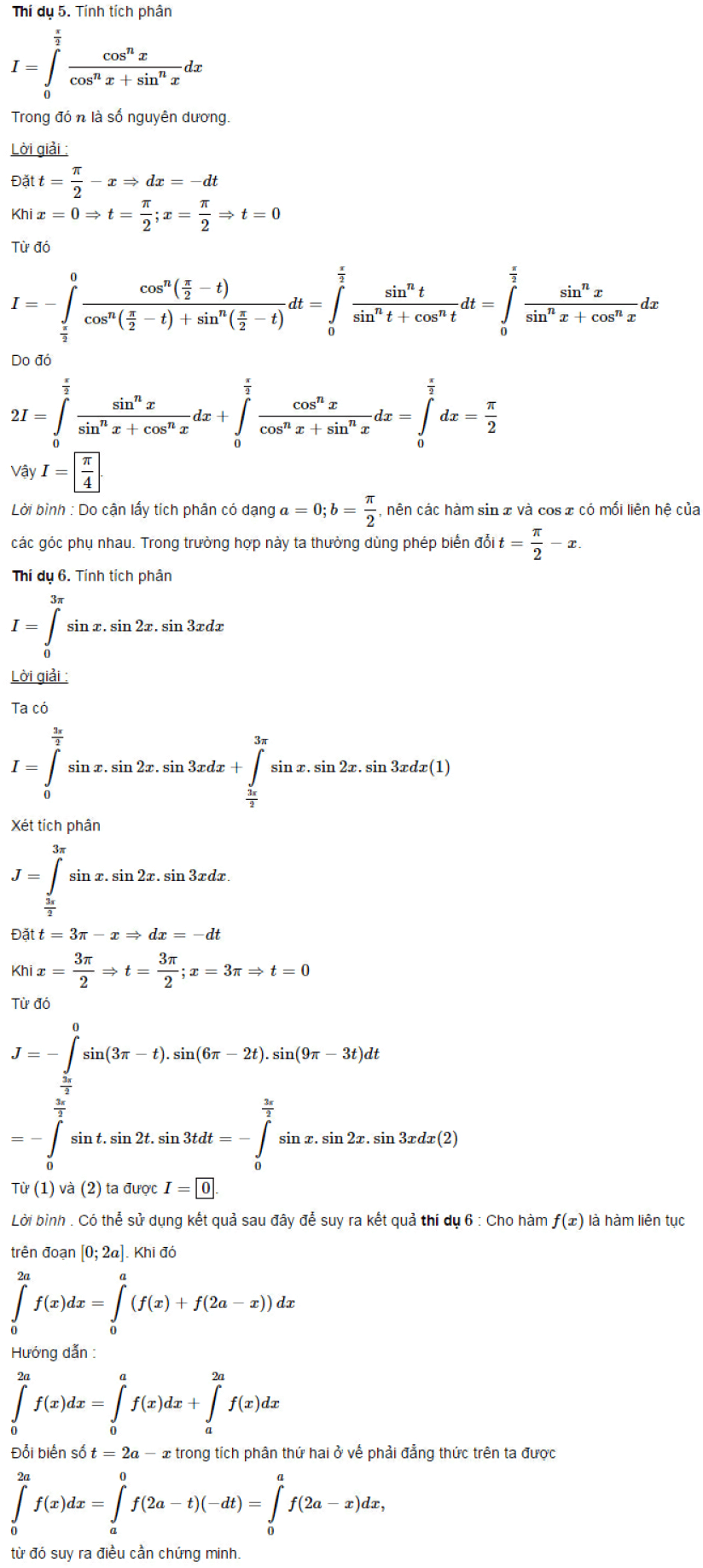
Bài tập tích phân lượng giác tự giải

Tính các tích phân lượng giác sau:

1. ${\displaystyle I={\int }_0^{\frac{\pi }{4}}{\tan }^{6}xdx}$

2. ${\displaystyle I={\int }_0^{\frac{\pi }{2}}\frac{\sin x+7\cos x+6}{4\sin x+3\cos x+5}dx}$

3. ${\displaystyle I={\int }_{\frac{\pi }{6}}^{\frac{\pi }{3}}\frac{1}{\sqrt[4]{{\sin }^{3}x\cdot {\cos }^{5}x}}dx}$

4. ${\displaystyle I={\int }_{\frac{\pi }{6}}^{\frac{\pi }{2}}\frac{{\cos }^{3}x+{\cos }^{5}x}{{\sin }^{2}x+{\sin }^{4}x}dx}$

5. ${\displaystyle I={\int }_{\frac{\pi }{4}}^{\frac{\pi }{3}}\frac{1}{{\sin }^{2}x\cdot {\cos }^{4}x}dx}$

• Tài liệu bồi dưỡng học sinh giỏi Toán 12

• Đề cương ôn tập Toán 12 học kỳ I năm 2013-2014

• Câu hỏi và bài tập trắc nghiệm Toán 12 – Nguyễn Phú Khánh, Huỳnh Đức Khánh

• Tóm tắt lý thuyết và giải nhanh Toán 12

• Tóm tắt một số công thức giải nhanh Toán 12

• Tóm tắt toàn bộ công thức giải tích 12

• Thủ thuật casio giải nhanh trắc nghiệm Toán 12