Cách tính khoảng cách giữa 2 mặt phẳng song song trong không gian
Để tính khoảng cách giữa hai mặt phẳng song song
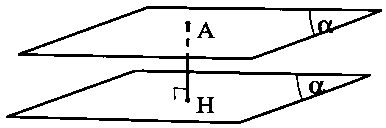
Công thức:
Bài tập áp dụng:
Câu 1: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
Chọn
Chọn đáp án B.
Nhận xét: Có thể sử dụng kết quả ở mục A – dạng 2 để chọn nhanh đáp án.
Câu 2: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
Do
Chọn đáp án C.
Nhận xét: Mọi mặt cầu
Câu 3: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
Ta có:
Chọn đáp án B.
Câu 4: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
Chọn
Theo giả thiết:
Chọn đáp án C.
Câu 5: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
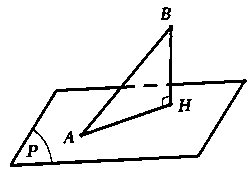
Gọi
Vậy
Suy ra
Chọn đáp án C.
Câu 6: Trong không gian với hệ tọa độ
A.
B.
C.
D. Vô số.
Lời giải:
Kiểm tra được:
Vậy tồn tại hai mặt phẳng chứa
+ Trường hợp 1: Mặt phẳng chứa
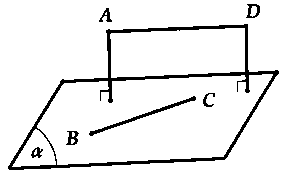
+ Trường hợp 2: Mặt phẳng chứa
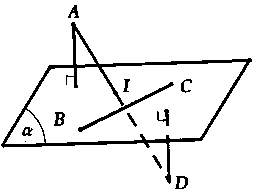
Chọn đáp án C.
Câu 7: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
Kiểm tra được:
+ Trường hợp 1: Mặt phẳng chứa
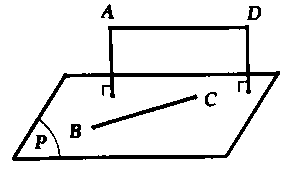
Mặt phẳng
+ Trường hợp 2: Mặt phẳng chứa
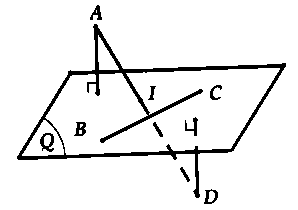
Trung điểm
Vậy
Chọn đáp án B.
Câu 8: Trong không gian với hệ tọa độ
A.
B.
C.
D.
Lời giải:
Kiểm tra được:
+ Trường hợp 1: Mặt phẳng chứa
Mặt phẳng
+ Trường hợp 2: Mặt phẳng chứa
Trung điểm
Mặt phẳng
Theo giả thiết
Vậy
Chọn đáp án D.
Tin tức - Tags: hình học không gian, khoảng cách, mặt phẳng, song songCách tính khoảng cách từ một điểm đến mặt phẳng trong không gian
Các bước khảo sát và vẽ đồ thị hàm số
Chứng minh các BĐT về tổng, tích của dãy số bằng phương pháp làm trội, làm giảm, phương pháp quy nạp
Ví dụ tính tích phân hàm số lượng giác có lời giải
Cách tính Tích phân hàm số hữu tỷ
Hà Nội quyết định bỏ môn thi thứ 4 tuyển sinh lớp 10 năm học 2020 – 2021
60 từ vựng tiếng Anh lớp 3 có phiên âm đầy đủ