Các khái niệm về tích phân

Tích phân là một khái niệm toán học,và cùng với nghịch đảo của nó vi phân (differentiation) đóng vai trò là 2 phép tính cơ bản và chủ chốt trong lĩnh vực giải tích (calculus).

1. Khái niệm tích phân

Có thể hiểu đơn giản tích phân như là diện tích hoặc diện tích tổng quát hóa. Giả sử cần tính diện tích một hình phẳng được bao bởi các đoạn thẳng, ta chỉ việc chia hình đó thành các hình nhỏ đơn giản hơn và đã biết cách tính diện tích như hình tam giác, hình vuông, hình thang, hình chữ nhật… Tiếp theo, xét một hình phức tạp hơn mà nó được bao bởi cả đoạn thẳng lẫn đường cong, ta cũng chia nó thành các hình nhỏ hơn, nhưng bây giờ kết quả có thêm các hình thang cong. Tích phân giúp ta tính được diện tích của hình thang cong đó.

Hoặc giải thích bằng toán học như sau: Cho một hàm f của một biến thực x và một miền giá trị thực [a, b]. Như vậy một tích phân xác định (definite integral) từ a đến b của f(x), ký hiệu là:

$ \displaystyle \int\limits_{a}^{b}{{f(x)dx}}$

được định nghĩa là diện tích của một vùng trong không gian phẳng xy được bao bởi đồ thị của hàm f, trục hoành, và các đường thẳng x = a và x = b, sao cho các vùng trên trung hoành sẽ được tính vào tổng diện tích, còn dưới trục hoành sẽ bị trừ vào tổng diện tích.

Ta gọi a là cận dưới của tích phân, còn b là cận trên của tích phân.

Cho F(x) là nguyên hàm của f(x) trong (a, b). Khi đó, tích phân bất định (indefinite integral) được viết như sau:

$ \displaystyle \int\limits_{{}}^{{}}{{f(x)dx}}=F(x) C$

Mọi định nghĩa tích phân đều phụ thuộc vào lý thuyết độ đo (measure). Ví dụ, tích phân Riemann dựa trên độ đo Jordan, còn tích phân Lebesgue dựa trên độ đo Lebesgue. Tích phân Riemann là định nghĩa đơn giản nhất của tích phân và thường xuyên được sử dụng trong vật lý và giải tích cơ bản.

2. Lược sử tích phân

Những phép tính tích phân đầu tiên đã được thực hiện từ cách đây 2.000 năm bởi Archimedes (287–212 trước Công nguyên), khi ông tính diện tích bề mặt và thể tích khối của một vài hình như hình cầu, hình parabol và hình nón. Phương pháp tính của Archimedes rất hiện đại dù vào thời ấy chưa có khái niệm về đại số, hàm số hay thậm chí cách viết số dạng thập phân.

Tích phân, vi phân và môn toán học của những phép tính này, giải tích, đã chính thức được khám phá bởi Leibniz (1646–1716) và Isaac Newton (1642–1727). Ý tưởng chủ đạo là tích phân và vi phân là hai phép tính nghịch đảo của nhau. Sử dụng mối liên hệ hình thức này, hai nhà toán học đã giải được một số lượng khổng lồ các bài toán quan trọng trong toán học, vật lý và thiên văn học.

J. B. Fourier (1768–1830) khi nghiên cứu sự truyền nhiệt đã tìm ra chuỗi các hàm lượng giác có thể dùng để biểu diễn nhiều hàm số khác. Biến đổi Fourier (biến đổi từ hàm số thành chuỗi các hàm lượng giác và ngược lại) và biến đổi tích phân ngày nay được ứng dụng rất rộng rãi không chỉ trong khoa học cơ bản mà cả trong Y học, âm nhạc và ngôn ngữ học.

Người đầu tiên lập bảng tra cứu các tích phân tính sẵn là Gauss (1777–1855). Ông đã cùng nhiều nhà toán học khác ứng dụng tích phân vào các bài toán của toán học và vật lý. Cauchy (1789–1857) mở rộng tích phân sang cho số phức. Riemann (1826–1866) và Lebesgue (1875–1941) là những người tiên phong đặt nền tảng lô-gíc vững chắc cho định nghĩa của tích phân.

Liouville (1809–1882) xây dựng một phương pháp để tìm xem khi nào tích phân vô định của hàm cơ bản lại là một hàm cơ bản. Hermite (1822–1901) tìm thấy một thuật toán để tính tích phân cho các hàm phân thức. Phương pháp này đã được mở rộng cho các phân thức chứa lô-ga-rít vào những năm 1940 bởi A. M. Ostrowski.

Vào những năm trước thời đại máy tính của thế kỷ 20, nhiều lý thuyết giúp tính các tích phân khác nhau đã không ngừng được phát triển và ứng dụng để lập các bảng tra cứu tích phân và biến đổi tích phân. Một số những nhà toán học đóng góp cho công việc này là G. N. Watson, E. C. Titchmarsh, E. W. Barnes, H. Mellin, C. S. Meijer, W. Grobner, N. Hofreiter, A. Erdelyi, L. Lewin, Y. L. Luke, W. Magnus, A. Apelblat, F. Oberhettinger, I. S. Gradshteyn, H. Exton, H. M. Srivastava, A. P. Prudnikov, Ya. A. Brychkov, và O. I. Marichev.

Vào năm 1969, R. H. Risch đã đóng góp một phát triển vượt bậc cho các thuật toán tính tích phân vô định bằng công trình của ông về lý thuyết tổng quát và ứng dụng trong tích phân các hàm cơ bản. Phương pháp đã chưa thể được ứng dụng ngay cho mọi hàm cơ bản vì cốt lõi của phương pháp là giải một phương trình vi phân khá khó. Những phát triển tiếp nối của nhiều nhà toán học khác đã giúp giải được phương trình vi phân này cho nhiều dạng hàm cơ bản khác nhau, ngày càng hoàn thiện phương pháp của Risch. Trong những năm 1980 đã có những tiến bộ mở rộng phương pháp này cho cả các hàm không cơ bản đặc biệt.

Từ thập niên 1990 trở lại đây, các thuật toán để tính biểu thức tích phân vô định được chuyển giao sang và tối ưu hoá cho tính toán bằng máy tính điện tử. Máy tính đã giúp loại bỏ sai sót con người, tạo nên khả năng tính hàng nghìn tích phân mới chưa bao giờ xuất hiện trong các bảng tra cứu. Một số phần mềm máy tính thương mại có khả năng tính biểu thức tích phân hiện nay là Mathematica, Maple,…

3. Thuật ngữ và kí pháp

Đối với trường hợp đơn giản nhất, tích phân của một hàm số thực f(x) trên x, được viết là:

$ \displaystyle \int\limits_{{}}^{{}}{{f(x)dx}}$

Với:

∫ là “sự tích phân”

f(x)dx gọi là biểu thức dưới dấu tích phân

dx biểu diễn việc tích phân trên x. dx được gọi là biến của tích phân. Trong topo toán học, việc biểu diễn chính xác là dx được tách ra khỏi hàm được tích phân (integrand) bằng một dấu cách.

Ta có thể thay đổi biểu thức f(x)dx bằng biểu thức f(t)dt hoặc bất kỳ một đối số nào như f(y)dy, f(u)du dưới dấu tích phân.

4. Một số tính chất của tích phân

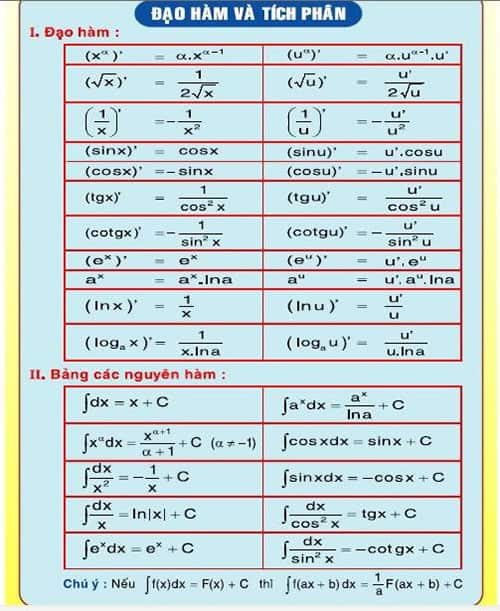
Các khái niệm về tích phân

Các khái niệm về tích phân

Tin tức - Tags: ,