Một số dạng Toán thực tế cấp THCS
Dưới đây là một số dạng Toán thực tế mà Trung tâm Gia sư Hà Nội muốn gửi tới các em học sinh khối trung học cơ sở. Chúc các em học tốt.
Mỗi dạng toán có bài tập ví dụ và các bài tập tự giải.
DẠNG 1: CÁC BÀI TOÁN KHÔNG LẬP PHƯƠNG TRÌNH HOẶC HỆ PHƯƠNG TRÌNH
1.1.Các bài toán có mối quan hệ giữa các đại lượng biểu thị bằng bảng, biểu đồ
Ví dụ: Bảng mô tả số cây ăn trái được trồng trên 5 cánh đồng. Nhìn vào bảng, em hãy trả lời câu hỏi sau:
| Loại cây ăn trái | Cánh đồng | |||
| A | B | C | D | |
| TÁO | 687 | 764 | 897 | 540 |
| CAM | 811 | 913 | 827 | 644 |
| LÊ | 460 | 584 | 911 | 678 |
a/ Số cam cánh đồng A nhiều hơn số cam cánh đồng D là bao nhiêu cây?
b/ Cánh đồng nào có tỉ lệ trồng lê cao nhất?
Một số bài toán tương tự:
1. Cho bảng số liệu sau: (đơn vị: triệu người)
| Năm | Tổng số | Chưa qua đào tạo | Qua đào tạo |
| 2013 | 48,30 | 40,49 | 7,81 |
| 2014 | 52,67 | 46,27 | 6,4 |
| 2015 | 54,32 | 47,53 | 6,79 |
Dựa vào bảng số liệu, em hãy trả lời các câu hỏi:
a/ Số người qua đào tạo năm 2015 giảm bao nhiêu so với năm 2013?
b/ Năm nào có % số người chưa qua đào tạo nhiều nhất? Tính % số người chưa qua đào tạo nhiều nhất đó.
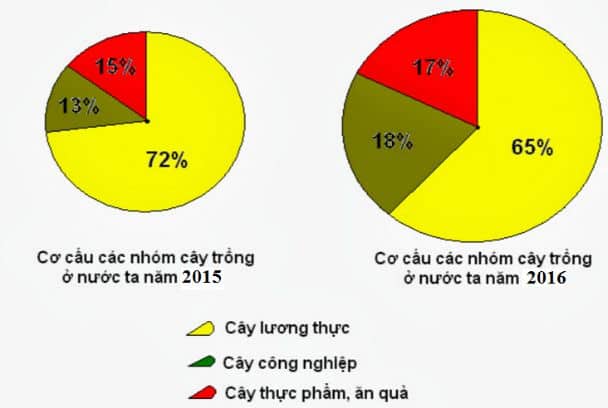
2. Hãy quan sát biểu đồ sau và trả lời câu hỏi.
a/ Cây lương thực năm 2016 tăng (hoặc giảm) bao nhiêu % so với năm 2015?
b/ So sánh tỉ lệ cây công nghiệp và tỉ lệ cây thực phẩm trong năm 2015 và 2016.
3. Theo quyết định của Bộ Công Thương ban hành, giá bán lẻ điện sinh hoạt từ ngày 16/03 sẽ dao động trong khoảng từ 1484 đến 2587 đồng mỗi kWh tùy bậc thang. Dưới đây là bảng so sánh biểu giá điện trước và sau khi điều chỉnh:
| MỨC SỬ DỤNG TRONG THÁNG (KWH) | GIÁ MỚI | GIÁ CŨ |
| 0-50 | 1484 | 1388 |
| 51-100 | 1533 | 1433 |
| 101-200 | 1786 | 1660 |
| 201-300 | 2242 | 2082 |
| 301-400 | 2503 | 2324 |
| 401 TRỞ LÊN | 2587 | 2399 |
a) Biết trong tháng 1 hộ A tiêu thụ 140 kWh thì hộ A phải trả bao nhiêu tiền?
b) Nếu hộ A trung bình mỗi tháng tiêu thụ 140 kWh thì theo giá mới số tiền phải trả tăng lên bao nhiêu trong 1 tháng?
1.2 Các bài toán về ứng dụng hình học
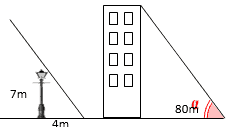
. Ví dụ 1: Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Gần đấy có một tòa nhà cao tầng có bóng trên mặt đất là 80m. Em hãy cho biết toà nhà đó có bao nhiêu tầng, biết rằng mỗi tầng cao 2m?
. Một số bài toán tương tự:
1. Một cây cau bị giông bão thổi mạnh làm gãy gập xuống làm ngọn cây chạm đất và tạo với mặt đất một góc 20o. Người ta đo được khoảng cách từ ngọn đến gốc cây cau là 7,5 (mét). Giả sử cây cau mọc vuông góc với mặt đất, hãy tính chiều cao của cây cau đó? (làm tròn đến chữ số thập phân thứ hai)
2. Một người quan sát đứng cách một tòa nhà một khoảng bằng 25m. Góc “nâng” từ chỗ người đó đứng đến nóc tòa nhà là 30o. Tính chiều cao của tòa nhà.
3. Một con thuyền qua khúc song với vận tốc 3 km/h mất hết 5 phút. Do dòng nước chảy mạnh nên đã đẩy con thuyền đi qua song trên đường đi tạo với bờ một góc 30o.Hãy tính chiều rộng của khúc sông.
4. Lúc 14h, một cây cột điện ngả bóng xuống mặt đường và có chiều dài của bóng đo được là 4m. Tại thời điểm đó ánh mặt trời tạo với mặt đất một góc 60o. Tính chiều cao của cây cột điện (làm tròn đến cm).
5. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34o và bóng của một tháp trên mặt đất dài 86m. Tính chiều cao của tháp (làm tròn đến mét).
6. Một người đi thuyền trên biển muốn đến ngọn hải đăng có độ cao 39m, người đó đứng trên mũi thuyền và đo được góc giữa mũi thuyền và tia nắng chiếu từ đỉnh ngọn hải đăng đến thuyền là 26o. Tính khoảng cách của thuyền đến ngọn hải đăng. (làm tròn đến m)
7. Các tia nắng mặt trời tạo với mặt đất một góc 30o và bóng của một tòa nhà cao tầng trên mặt đất dài 54m .Tính chiều cao của tòa nhà ? (làm tròn lấy 3 chữ số thập phân)
8. Nhà bạn Minh có một chiếc thang dài 4 mét. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là 65o (tức là đảm bảo thang không bị đổ khi sử dụng).
9. Để chuẩn bị khai giảng năm học mới ở trường , bác bảo vệ kiểm tra cột cờ thì phát hiện dây kéo cờ bị hỏng nên phải thay dây mới. Để mua dây kéo cờ không bị thừa nên trường nhờ một giáo viên dạy toán đo chiều cao cột cờ. Giáo viên không dùng thước đo chiều cao cột cờ mà dùng giác kế ngắm cột cờ với góc 36o50’ , chân giác kế cách cột cờ là 9,6 m. Vậy dây kéo cờ bao nhiêu mét. ( kết quả làm tròn đến chữ số thập phân thứ hai)
10. Một cây dương mọc đơn độc giữa đồng, bỗng nhiên gió thổi mạnh làm nó gẫy gập xuống , ngọn cây chạm đất cách gốc 4m, từ gốc đến chỗ cây gãy 3m. Hỏi cây dương cao bao nhiêu mét ?
1.3 Các bài toán dùng sơ đồ Ven
. Ví dụ 4: Để phục vụ cho Hội nghị quốc tế, ban tổ chức huy động 30 cán bộ phiên dịch tiếng Anh, 25 cán bộ phiên dịch tiếng Pháp, trong đó có 12 cán bộ phiên dịch được cả 2 thứ tiếng Anh và Pháp. Hỏi:
a/ Ban tổ chức đã huy động bao nhiêu cán bộ phiên dịch cho Hội nghị đó?
b/ Có bao nhiêu cán bộ chỉ dịch được tiếng Anh, chỉ dịch được tiếng Pháp?
Bài tương tự:
1. Lớp 9A có 30 em tham gia hội tiếng Anh và tiếng Trung. Trong đó có 25 em nói được tiếng Anh và 18 em nói được tiếng Trung. Hỏi có bao nhiêu em nói được cả hai thứ tiếng?
2. Trong hội nghị có 100 đại biểu tham dự, mỗi đại biểu nói được một hoặc hai trong ba thứ tiếng: Nga, Anh và Pháp. Có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu chỉ nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?
3. Người ta điều tra trong một lớp học có 40 học sinh thì thấy có 30 học sinh thích Toán, 25 học sinh thích Văn, 2 học sinh không thích cả Toán và Văn. Hỏi có nhiêu học sinh thích cả hai môn Văn và Toán?
4. Trên 1 hội nghị các đại biểu sử dụng một hoặc hai trong 3 thứ tiếng : Nga, Anh hoặc Pháp. Có 30 đại biểu nói được tiếng Pháp, 35 đại biểu chỉ nói được tiếng Anh, 20 đại biểu chỉ nói được tiếng Nga và 15 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi hội nghị đó có bao nhiêu đại biểu tham dự?
5. Đội tuyển thi học sinh giỏi của tỉnh X có 25 em thi Văn và 27 em thi toán, trong đó có 18 em vừa thi Văn vừa thi toán. Hỏi đội tuyển học sinh giỏi 2 môn Văn và Toán của tỉnh X có bao nhiêu em?
DẠNG 2: CÁC BÀI TOÁN LẬP PHƯƠNG TRÌNH HOẶC HỆ PHƯƠNG TRÌNH
2.1 Các bài toán lập phương trình, hệ phương trình quen thuộc:
Ví dụ 1. Một miếng đất hình chữ nhật có chu vi là 40m và chiều dài gấp 3 lần chiều rộng. Tính diện tích miếng đất.
. Một số bài toán tương tự:
1. Một miếng đất hình chữ nhật có chu vi là 40m và chiều dài gấp 3 lần chiều rộng. Tính diện tích miếng đất
2. Một miếng đất hình chữ nhật có chu vi là 120m. Biết tỉ số 2 cạnh của hình chữ nhật là 5 : 3. Tính độ dài của hai cạnh hình chữ nhật.
3. Một hình chữ nhật có tỉ số chiều dài và chiều rộng là 5/4 và chu vi là 36 m. Tính diện tích hình chữ nhật.
4. Một mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng 30m và có chu vi là 104m. Tính diện tích mảnh vườn.
5. Mỗi cạnh của hình vuông được tăng thêm 2cm. Trong lúc đo diện tích của nó tăng thêm 16cm2. Chiều dài của mỗi cạnh hình vuông trước khi chưa tăng là bao nhiêu?
6. Một khu vườn hình chữ nhật có chu vi 280 m. Người ta làm một lối đi xung quanh vườn (thuộc đất vườn) rộng 2m, diện tích còn lại để trồng trọt là 4256 m2. Tính kích thước (các cạnh) của khu vườn đó
Ví dụ 2. Một người đi xe máy từ A đến B với vân tốc trung bình 30 km/h. Khi đến B người đó nghỉ 20 phút rồi quay trở về A với vận tốc trung bình 25 km/h. Tính quãng đường AB, biết thời gian cả đi và về là 5 giờ 50 phút.
. Bài toán tương tự:
1. Một Ô tô dự định đi từ tỉnh A đến tỉnh B với vận tốc trung bình 40 km/ h. Lúc đầu ô tô đi với vận tốc đó, khi còn 60 km nữa thì được nửa quãng đường AB, người lái xe tăng thêm vân tốc 10 km/h trên quãng đường còn lại, do đó Ô tô đến B sớm hơn 1 giờ so với dự định. Tính quãng đường AB.
2. Một Ô tô dự định đi từ A đến B trong thời gian nhất định nếu xe chạy với vận tốc 35 km/h thì đến chậm mất 2 giờ. Nếu xe chạy với vận tốc 50 km/h thì đến sớm hơn 1 giờ. Tính quãng đường AB và thời gian dự định đi lúc đầu.
3. Một chiếc thuyền khởi hành từ bến sông A, sau 5 giờ 20 phút một ca nô chạy từ bến sông A đuổi theo và gặp thuyền cách bến A 20 km. Hỏi vận tốc của thuyền, biết rằng ca nô chạy nhanh hơn thuyền 12 km/h.
4. Quãng đường AB dài 270 km. Hai Ô tô khởi hành cùng một lúc đi từ A đến B. Ô tô thứ nhất chạy nhanh hơn Ô tô thứ hai 12 km/h, nên đến trước Ô tô thứ hai 40 phút. Tính vận tốc của mỗi Ô tô.
5. Hai Ô tô khởi hành cùng một lúc từ địa điểm A đến địa điểm B dài 240 km. Mỗi giờ Ô tô thứ nhất chạy chanh hơn Ô tô thứ hai 12 km/h nên đến địa điểm B trước Ô tô thứ hai là 100 phút. Tính vận tốc của mỗi Ô tô.
Ví dụ3: Lớp 9A có số học sinh nam bằng 3/4 số học sinh nữ và ít hơn số học sinh nữ là 6 học sinh. Hỏi lớp 9A có bao nhiêu học sinh?
. Bài toán tương tự:
1. Trong một lớp học tỉ số hs nữ và nam là 5/7 , biết hs nam nhiều hơn hs nữ là 6 em . Hỏi lớp có bao nhiêu học sinh?
2. Tìm số HS lớp 7A và 7B biết số học sinh lớp 7B ít hơn lớp 7A là 5 học sinh và tỉ số học sinh của lớp 7A và 7B là 7 : 6.
3. Sơ kết học kì I lớp 7A có số học sinh giỏi, khá, trung bình tỉ lệ với các số 5; 7; 3, không có học sinh yếu, kém. Tính số học sinh mỗi loại biết lớp có 45 học sinh.
4. Trong khu vườn có trồng 2 loại cây là cam và chanh. Số cây cam bằng 2/3 số cây chanh. Tìm số cây cam và số cây chanh được trồng trong vườn biết tổng số cây cam và chanh là 45 cây.
2.2 Các bài toán về thuế GTGT, tiền bạc
Ví dụ 1. Một người mua một món hàng và phải trả tổng cộng 2.915.000 đồng kể cả thuế giá trị gia tăng (VAT) là 10%. Hỏi nếu không kể thuế VAT thì người đó phải trả bao nhiêu tiền cho món hàng.
Ví dụ 2. Bạn Nam đem 20 tờ tiền giấy gồm hai loại 2.000 đồng và 5.000 đồng đến siêu thị mua một món quà có giá trị 78.000đồng và được thối lại 1.000 đồng. Hỏi có bao nhiêu tờ giấy tiền mỗi loại .
Ví dụ 3. Giá bán một chiếc ti vi giảm giá 2 lần, mỗi lần giảm 10% so với giá đang bán, sau khi giảm giá hai lần thì giá còn lại là 16.200.000 đồng. Vậy giá bán ban đầu của chiếc ti vi là bao nhiêu?
Ví dụ4. Một người gửi tiết kiệm 200 triệu đồng vào tài khoản ngân hàng Nam Á. Có 2 sự lựa chọn: người gửi có thể nhận được lãi suất 7% một năm hoặc nhận tiền thưởng ngay là 3 triệu với lãi suất 6% một năm. Lựa chọn nào tốt hơn sau 1 năm? Sau 2 năm?
. Kiến thức liên quan: giải bài toán bằng cách lập phương trình (lớp 8)
. Bài giải: . Gọi a (đồng) là số tiền vốn ban đầu (a > 0), lãi suất x%/năm:
. Số tiền lãi nhận được sau 1 năm:
. Số tiền nhận được sau 1 năm gồm vốn lẫn lãi:
. Số tiền lãi nhận được sau 2 năm:
. Số tiền nhận được sau 2 năm gồm vốn lẫn lãi:
. Với lãi suất 7%
. Số tiền nhận được sau 1 năm gồm vốn lẫn lãi: 200 triệu. (7% + 1) = 214 triệu đồng
. Số tiền nhận được sau 2 năm gồm vốn lẫn lãi: 200 triệu. (7% + 1)2 = 22 980 000 đồng
. Với lãi suất 6%
. Số tiền nhận được sau 1 năm gồm vốn lẫn lãi và tiền thưởng:
200 triệu. (6% + 1) + 3 triệu = 215 triệu đồng
. Số tiền nhận được sau 2 năm gồm vốn lẫn lãi và tiền thưởng:
200 triệu. (6% + 1)2 + 3 triệu = 227 720 000 đồng
Vậy: gửi 1 năm với lãi suất 6% có lợi hơn; gửi 2 năm với lãi suất 7% có lợi hơn.
. Bài tương tự:
1. Ông Luân gửi tiết kiệm 200 triệu VNĐ vào ngân hàng, biết rằng sau một năm tiền lãi tự nhập thêm vào vốn và lãi suất không đổi là 7% /năm. Hỏi sau 2 năm ông lĩnh được số tiền cả vốn lẫn lãi là bao nhiêu VNĐ?
2. Để thực hiện chương trình ngày “Black Friday” 25/11/2016. Một cửa hàng điện tử thực hiện giảm giá 50% trên 1 tivi cho lô hàng tivi gồm có 40 cái với giá bán lẻ trước đó là 6500000 đ/cái. Đến trưa cùng ngày thì cửa hàng đã bán được 20 cái khi đó cửa hàng quyết định giảm thêm 10% nữa thì số tivi còn lại.
a/ Tính số tiền mà cửa hàng thu được khi bán hết lô hàng tivi.
b/ Biết rằng giá vốn là 3050000đ/cái tivi. Hỏi cửa hàng có lời hay lỗ khi bán hết lô hàng tivi đó?
3. Cô An đi siêu thị mua một món hàng đang khuyến mãi giảm giá 20%, cô có thẻ khách hàng thân thiết của siêu thị nên được giảm thêm 2% trên giá đã giảm nữa, do đó cô chỉ phải trả 196.000 đồng cho món hàng đó. Hỏi giá ban đầu của món hàng nếu không khuyến mãi là bao nhiêu?
4. Bạn Bình đi nhà sách và mang theo một số tiền vừa đủ để mua 5 quyển tập và 3 cây viết. Nhưng khi mua, giá một quyển tập mà bạn Bình định mua đã tăng lên 800 đồng, còn giá tiền một cây viết thì giảm đi 1000đồng. Hỏi để mua 5 quyển tập và 3 cây viết như dự định ban đầu thì bạn Bình còn dư hay thiếu bao nhiêu tiền?
2.3 Các bài toán về giá cước Taxi

2.4 Toán sử dụng các kiến thức vậy lý, hóa học

. Một số bài toán tương tự:
1. Biết rằng 200g một dung dịch chứa 50g muối. Hỏi phải pha thêm bao nhiêu gam nước vào dung dịch đó để được một dung dịch chứa 20% muối?
2. Người ta pha 3kg nước nóng ở nhiệt độ 900C và 2kg nước lạnh ở nhiệt độ 200C. Hỏi nhiệt độ nước sau khi pha là bao nhiêu.
3. Khi trộn 8g chất lỏng M với 6g chất lỏng N có khối lượng riêng nhỏ hơn 200kg/m3 thì được một hỗn hợp có khối lượng riêng 700kg/m3. Tính khối lượng riêng của mỗi chất lỏng.
4. Vào thế kỷ III trước công nguyên, vua xứ Xi-ra-cut giao cho Ac-si-met kiểm tra chiếc mũ bằng vàng của nhà vua có bị pha thêm bạc hay không. Chiếc mũ có trọng lượng 5niuton (theo đơn vị hiện nay), nhúng trong nước thì trọng lượng giảm 0,3 niuton. Biết rằng khi cân trong nước, vàng giảm trọng lượng, bạc giảm trọng lượng. Hỏi chiếc mũ chứa bao nhiêu gam vàng, bao nhiêu gam bạc?
5. Hai dung dịch có khối lượng tổng cộng bằng 220kg. Lượng muối trong dung dịch I là 5kg, lượng muối trong dung dịch II là 4,8kg. Biết nồng độ muối trong dung dịch I nhiều hơn nồng độ muối trong dung dịch II là 1%. Tính khối lượng mỗi dung dịch nói trên.
2.5 Các bài toán thực tế khác
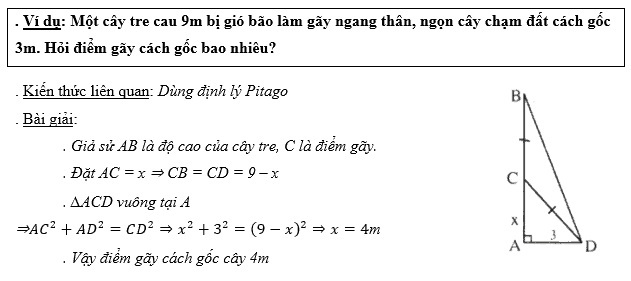
. Một số bài toán tương tự:
1. Một cây dương mọc đơn độc giữa đồng, bỗng nhiên gió thổi mạnh làm nó gẫy gập xuống , ngọn cây chạm đất cách gốc 4m, từ gốc đến chỗ cây gãy 3m. Hỏi cây dương cao bao nhiêu mét ?
2. Hai cây cọ mọc đối diện nhau ở hai bờ sông, một cây cao 30m, một cây cao 20m. Trên đỉnh mỗi cây có 1 con chim đang đậu. Chợt có 1 con cá xuất hiện trên sông giữa hai cây cọ. Cả hai con chim lập tức bay xuống vồ mồi cùng một lúc. Hỏi con cá cách gốc mỗi cây cọ bao nhiêu mét biết rằng hai gốc cây cách nhau 50m. ?
Tin tức - Tags: bài toán thực tế, THCSTóm tắt kiến thức Sinh học lớp 12
Bài thi kiểm tra năng lực giáo viên giỏi cấp trường tiểu học năm 2016-2017
Các dạng toán: Tính nhanh giá trị của biểu thức và cách giải
Mẹo làm bài tập tích phân
Các khái niệm về tích phân
Tích phân của hàm chứa dấu giá trị tuyệt đối
Phương pháp tích phân từng phần giải bài toán tích phân