Dạng bài tập tiếp tuyến chung của hai đường tròn – Ôn thi vào 10 môn Toán

Bài viết hướng dẫn học sinh lớp 9 ôn thi vào lớp 10 môn Toán giải dạng bài tập toán có tiếp tuyến chung của hai đường tròn.

Để làm được dạng bài tập này, các em cần nắm rõ tính chất tiếp tuyến của đường tròn và định lí Ta-lét. Các em nên đọc lại các bài viết này:

– Dấu hiệu nhận biết tiếp tuyến của đường tròn

– Ôn tập: Tiếp tuyến của đường tròn

– Cách chứng minh đường thẳng là tiếp tuyến của đường tròn

– Định lí Talet trong tam giác

– Định lí đảo và hệ quả của định lí Talet

II. Ví dụ

Ví dụ 1. Cho hai đường tròn ngoài nhau (O1, R1) và (O2, R2). Tiếp tuyến chung ngoài d và tiếp tuyến chung trong d’ cắt đường nối tâm O1O2 lần lượt tại S và I. Chứng minh:

$\displaystyle\frac{I O_{1}}{I O_{2}}=\frac{S O_{1}}{S O_{2}}=\frac{R_{1}}{R_{2}}$

Giải

Dạng bài tập tiếp tuyến chung của hai đường tròn - Ôn thi vào 10 môn Toán

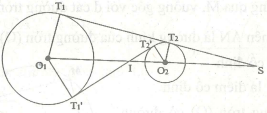
d là tiếp tuyến chung ngoài của (O1) và (O2), tiếp điểm T1 và T2, ta có:

$\displaystyle\left\{\begin{array}{l}O_{1} T_{1} \perp d \\ O_{2} T_{2} \perp d\end{array} \Rightarrow O_{1} T_{1} / / O_{2} T_{2}\right.$

Theo định lí Vi-ét, ta có:

$\displaystyle\frac{S 0_{1}}{S O_{2}}=\frac{O_{1} T_{1}}{O_{2} T_{2}} \Rightarrow \frac{S O_{1}}{S O_{2}}=\frac{R_{1}}{R_{2}}$  (1)

Tương tự: d’ là tiếp tuyến chung trong của (O1) và (O2), tiếp điểm là T1 và T2′, ta có:

$\displaystyle\left\{\begin{array}{l}O_{1} T_{1}^{\prime} \perp d^{\prime} \\ O_{2} T_{2}^{\prime} \perp d^{\prime}\end{array} \Rightarrow O_{1} T_{1} / / O_{2} T_{2}\right.$

Theo định lí Vi-ét, ta có:

$\displaystyle\frac{I O_{1}}{I O_{2}}=\frac{O_{1} T_{1}}{O_{2} T_{2}} \Rightarrow \frac{I O_{1}}{I O_{2}}=\frac{R_{1}}{R_{2}}$  (2)

Từ (1) và (2) suy ra đpcm.

Ví dụ 2. Cho nửa đường tròn tâm O đường kính AB và một điểm M bất kì trên nửa đường tròn (O). H là chân đường vuông góc hạ từ M xuống AB. Vẽ hai nửa đường tròn tâm I đường kính AH và tâm K đường kính BH nằm phía trong nửa đường tròn (O), cắt MA, MB lần lượt tại P, Q.

a. Chứng minh MH = PQ

b. Chứng minh PQ là tiếp tuyến chung của hai nửa đường tròn (I) và (K).

Giải

a. Ba điểm M, P, Q lần lượt nằm trên ba nửa đường tròn (O), (I) và (K) nên góc AMB bằng 90º, góc APH bằng 90º.

Suy ra: góc MPH bằng 90º, góc MQH bằng 90º

⇒ Tứ giác MPHQ là hình chữ nhật (tứ giác có ba góc vuông).

⇒ MH = PQ (hai đường chéo của hình chữ nhật).

b. Theo câu a tứ giác MPHQ là hình chữ nhật ⇒ góc HPQ bằng góc MHP (1)

IP = IH (bán kính của nửa đưởng tròn tâm I) ⇒ góc IPH bằng góc IHP     (2)

$M H \perp A B \Rightarrow \widehat{M H P}+\widehat{I H P}=90^{\circ}$  (3)

Từ (1), (2) và (3) Suy ra: $\displaystyle\widehat{M P H}=\widehat{I P H}=90^{\circ}$

⇒ PQ ⊥ IP

⇒ PQ là tiếp tuyến của nửa đường tròn (I).

Tương tự: PQ cũng là tiếp tuyến của nửa đường tròn (K).

Vậy PQ là tiếp tuyến chung của hai nửa đường tròn (I) và (K).

III. Bài tập áp dụng có lời giải

Bài 1. Cho hai đường tròn (O, 3cm) và (O’, 4cm) ngoài nhau. Tiếp tuyến chung ngoài d và tiếp tuyến chung trong d’ cắt OO’ lần lượt tại I và J. Biết OO’ = 14cm. Tính độ dài đoạn thẳng IJ.

Giải:

(Xem lại hình vẽ. Ví dụ 1)

Áp dụng:

$\displaystyle\frac{I O}{I O^{\prime}}=\frac{J O}{J O^{\prime}}=\frac{R}{R^{\prime}}=\frac{4}{3}$

Theo đề bài: OO’ = 14cm

Tính được: IJ = IO’ + O’J = 52 + 6 = 58cm.

Bài 2. Cho nửa đường tròn tâm O đường kính AB. Một tiếp tuyến tại điểm di động M trên nửa đường tròn cắt tiếp tuyến Ax, By tại C và D. Các đường thẳng vuông góc với CD tại C và D cắt AB tại N và P. Đường tròn tâm N và đường tròn P tiếp xúc với nhau tại O. Chứng minh CD là tiếp tuyến chung của đường tròn (N) và đường tròn (P).

Giải:

Đường tròn tâm N tiếp xúc với đường tròn tâm P tại O nên đường tròn tâm N có bán kính NO, đường tròn tâm N có bán kính PO.

Kẻ OC’ ⊥ CN tại C’

⇒ Tứ giác MCC’O là hình chữ nhật (vì 3 góc M, C, C’ bằng 90º)

⇒ OC’ = MC

Mà MA = MC (tính chất của hai tiếp tuyến cắt nhau)

Nên OC’ = MA

Dạng bài tập tiếp tuyến chung của hai đường tròn - Ôn thi vào 10 môn Toán

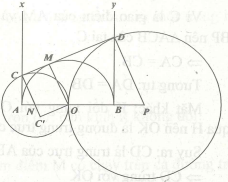
Suy ra: △NAC = △NC’O (tam giác vuông có một góc nhọn và một cạnh góc vuông bằng nhau).

⇒ NC = NO

⇒ CD là tiếp tuyến của đường tròn (N)

Tương tự: CD là tiếp tuyến của đường tròn (P)

Vậy CD là tiếp tuyến của đường tròn (N) và đường tròn (P).

Bài 3. Cho hai đường tròn (O, 2R) và (O’, R) tiếp xúc ngoài với nhau tại T. Gọi d là tiếp tuyến chung ngoài của hai đường tròn , A và B lần lượt là tiếp điểm của d với (O) và (O’).

a. Tính AB theo R. Chứng minh đường tròn đường kính AB tiếp xúc với OO’ tại T.

b. Đường tròn (I, R’) tiếp xúc với đường tròn (O), (O’) và tiếp xúc với AB tại C. Tính R’ theo R.

Giải:

a. – Tính AB theo R

Kẻ O’O” // AB cắt OA tại O”.

⇒ O”A = O’B = R và O’O” = AB

△OO’O” vuông tại O” nên:

$\displaystyle O{{{O}’}^{2}}={O}'{{{O}”}^{2}}+{O}'{{{O}”}^{2}}$

⇒ $\displaystyle(3 R)^{2}=R^{2}+A B^{2} \Rightarrow \mathrm{AB}=2 \mathrm{R} \sqrt{2}$

– Chứng minh đường tròn đường kính AB tiếp xúc với OO’ tại T.

Gọi J là giao điểm của AB và tiếp tuyến trong của hai đường tròn (O) và (O’) nên

$\displaystyle AC\text{ }=\text{ }2~\sqrt{{R.{R}’}}$

Tương tự: $\displaystyle BC\text{ }=\text{ }2~\sqrt{2}.\sqrt{{R.{R}’}}$

Dạng bài tập tiếp tuyến chung của hai đường tròn - Ôn thi vào 10 môn Toán

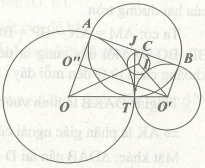
Mà AB = AC + CB nên:

$\displaystyle2 \sqrt{R \cdot R^{\prime}}+2 \sqrt{2} \cdot \sqrt{R \cdot R^{\prime}}=2 R \cdot \sqrt{2}$

⇔ $\displaystyle\sqrt{R^{\prime}} \cdot \sqrt{R}(1+\sqrt{2})=R \sqrt{2} \Leftrightarrow R^{\prime}=\frac{\sqrt{2}}{1+\sqrt{2}} R$

Bài 4. Cho đường tròn (O, R) và hai điểm A, B cố định trên (O) sao cho OA vuông góc với OB. Vẽ các dây cung bằng nhau AM, AN, BP, BQ. Gọi H là trung điểm của AB, K đối xứng với O qua H. Gọi C là giao điểm của AM và BP, D là giao điểm của AN và BQ (C nằm ngoài O và H).

a. Chứng minh ba điểm C, D, H thẳng hàng.

b. Chứng minh AM, AN, BP, BQ là các tiếp tuyến chung của hai đường tròn. Tìm hệ thức liên hệ giữa các bán kính của hai đường tròn nói trên với R.

Giải:

a. Ta có: AM = AN = BP = BQ nên tâm O cách đều 4 dây AM, AN, BP, BQ

Vì C là giao điểm của AM và BP nên △ACB cân tại C.

⇒ CA = CB

Tương tự: DA = DB

Mặt khác: K đối xứng với O qua H nên OK là đường trung trực của AB

Suy ra: CD là đường trung trực của AB

⇒ CD trùng với OK

Vậy ba điểm C, D, H nằm trên OK hay ba điểm C, D, H thẳng hàng.

b. – Chứng minh 4 dây cung AM, AN, BP, BQ là các tiếp tuyến chung của hai đường tròn.

Ta có: AM = AN = BP = BQ nên tâm O cách đều 4 dây cung AM, AN, BP, BQ ⇒ Mỗi dây cung là tiếp tuyến của đường tròn (O), bán kính r là khoảng cách từ O đến mỗi dây (1)

Tứ giác OAKB là hình vuông ⇒ góc AOK bằng 90º

⇒ AK là phân giác ngoài của góc DAC

Mặt khác: △DAB cân tại D có DK là trung trực của AB nên DK là phân giác góc ADB.

Do đó: K là tâm đường tròn bàng tiếp trong góc D của △DAM

⇒ AM, AN, BP, BQ là tiếp tuyến của đường tròn (K), bán kính r’ là khoảng cách từ K đến mỗi dây cung (2)

Từ (1) và (2) suy ra: 4 dây cung AM, AN, BP, BQ là các tiếp tuyến chung của hai đường tròn (O, r) và (K, r’)

– Hệ hức giữa r và r’

Kẻ OI và KJ cùng vuông góc với DB.

Ta có: OI = r, KJ = r’

△OIB = △BJK (cạnh huyền – góc nhọn) nên IB = JK

△OIB vuông tại I cho: $\displaystyle O{{I}^{2}}+I{{B}^{2}}=O{{B}^{2}}$

⇒ $\displaystyle {{r}^{2}}+{{{r}’}^{2}}={{R}^{2}}$ (hệ thức cần tìm).

Ôn thi Toán vào lớp 10 - Tags: ,