Cách chứng minh hai tam giác bằng nhau qua các ví dụ

Để chứng minh hai tam giác bằng nhau chúng ta có thể chứng minh bằng cách áp dụng các trường hợp cạnh – góc – cạnh, góc – cạnh – góc, cạnh – cạnh – cạnh.

Tùy từng bài tập mà sử dụng cách nào cho hợp lý. Chúng ta cùng làm các ví dụ tương ứng với các trường hợp xem nhé.

Phương pháp chứng minh 2 tam giác bằng nhau (cạnh – góc – cạnh)

Bài 1: Cho tam giác ABC có M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm N sao cho MN = MA. chứng minh : c) AC = BN. b) AB // NC

Giải.

a) AC = BN :

Xét ΔACM và ΔNBM, ta có :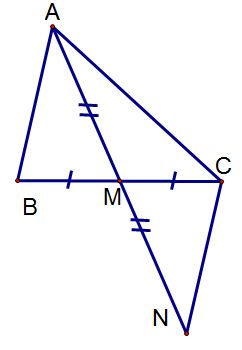 Cách chứng minh hai tam giác bằng nhau qua các ví dụ

MB = MC (M là trung điểm của BC)

$\widehat{AMC}=\widehat{NMB}$ (đối đỉnh).

MA = MN (gt).

=> ΔACM = ΔNBM (c -g -c)

=> AC = BN b) BC vuông góc DE :

Xét ΔABM và ΔNCM, ta có :

MB = MC (M là trung điểm của BC)

$\widehat{AMB}=\widehat{NMC}$ (đối đỉnh).

MA = MN (gt).

=> ΔABM = ΔNCM (c -g -c)

=> $\widehat{BAM}=\widehat{CNM}$

Mà : $\widehat{BAM}; \widehat{CNM}$ ở vị trí so le trong. => AB // NC.

Bài 2: Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại D Trên cạnh BC lấy điểm E sao cho BE = AB.chứng minh : BC vuông góc DE.

Giải.

Xét ΔABD và ΔEBD, ta có :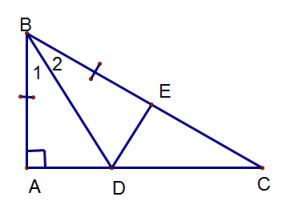

BE = AB (gt)

$\widehat{B_1}=\widehat{B_2}$ (BD là phân giác góc B).

BD cạnh chung.

=> ΔABD = ΔEBD (c -g -c)

=> $\widehat{BAD}=\widehat{BED}$

Mà : $\widehat{BAD}=90^0$ (gt)

=> $\widehat{BED}=90^0$ Hay BC vuông góc DE.

Bài 3: Cho tam giác ABC . gọi D, E lần lượt là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh : A là trung điểm của MN.

Giải.

Xét ΔBCD và ΔBMD, ta có :

DB = DA (D là trung điểm của AB)

$\widehat{D_1}=\widehat{D_2}$ (đối đỉnh).

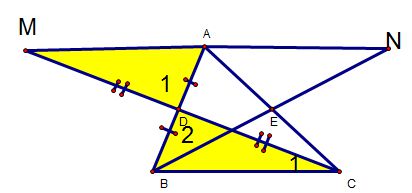
DC = DM (gt).

=> ΔBCD = ΔBMD (c -g -c)

=> $\widehat{C_1}=\widehat{M}$ và BC = AM.

Mà : $\widehat{C_1}; \widehat{M}$ ở vị trí so le trong. => BC // AM.

Cmtt, ta được : BC // AN và BC = AN.

ta có : BC // AM (cmt) và BC // AN (cmt)

=> A, M. N thẳng hàng. (1)

BC = AM và BC = AN => AM = AN (2).

Từ (1) và (2), suy ra : A là trung điểm của MN.

Phương pháp chứng minh 2 tam giác bằng nhau (góc – cạnh – góc)

Bài 1: Cho tam giác ABC. Gọi D là trung điểm AC. Từ A vẽ đường thẳng song song BC cắt BD tại E. trên cạnh BC lấy M, đường thẳng DM cắt AE tại N Chứng minh :

AE = BC.
D là trung điểm MN.
AB // EC

Giải.

1) AE = BC :

Xét ΔADE và ΔCDB, ta có :

$\widehat{A_1}=\widehat{C_1}$ (so le trong).

DA = DC (D là trung điểm AC)

$\widehat{ADE}=\widehat{CDB}$ (đối đỉnh).

=> ΔADE = ΔCDB (g – c – g)

=> AE = BC.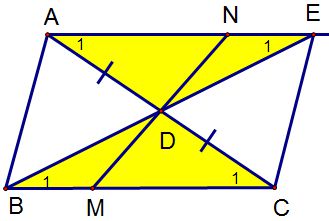

2) D là trung điểm MN :

Xét ΔNDE và ΔMDB, ta có :

$\widehat{E_1}=\widehat{B_1}$ (so le trong).

DE = DB (ΔADE = ΔCDB)

$\widehat{EDE}=\widehat{MDB}$ (đối đỉnh).

=> ΔADE = ΔCDB (g – c – g)

=> DM = DN

Hay D là trung điểm MN.

3) AB // EC :

Xét ΔADB và ΔCDE, ta có :

DA = DC (D là trung điểm AC)

$\widehat{ADB}=\widehat{CDE}$ (đối đỉnh).

DE = DB (ΔADE = ΔCDB)

=> ΔADE = ΔCDB (c – g – c)

=> $\widehat{BAD}=\widehat{DCE}$

Mà : $\widehat{BAD};\widehat{DCE}$ ở vị trí so le trong.

=> AB // EC.

Phương pháp chứng minh 2 tam giác bằng nhau (cạnh – cạnh – cạnh)

Bài 1:

Cho tam giác ABC có AB =AC, M là trung điểm của BC. Chứng minh rằng AM vuông góc BC.

Giải.

Xét ΔAMB và ΔAMC, ta có :

AB =AC (gt)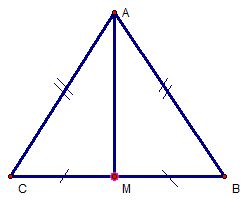

MB = MC (M là trung điểm của BC)

AM cạnh chung

=> ΔAMB = ΔAMC (c – c – c)

=> $\widehat{AMB} =\widehat{AMC}$

Mà : $\widehat{AMB} \widehat{AMC} =180^0$ (hai góc kề bù)

=> $\widehat{AMB} =\widehat{AMC}=90^0$

Hay AM $\bot$ BC.

Bài 2:

Cho tam giác ABC có AB =AC, trong tam giác ABC lấy điểm M sao cho MB = MC . Chứng minh rằng AM là phân giác của $\widehat{BAC}$ .

Giải.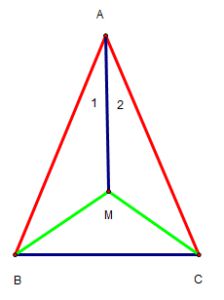

Xét ΔABM và ΔACM , có :

AB = AC (gt)

AM = BM (gt)

AM cạnh chung.

=> ΔABM = ΔACM (c – c – c)

=> $\widehat{A_1} =\widehat{A_2}$ (góc tương ứng)

VẬY : AM là phân giác của $\widehat{BAC}$

Bài 3:

Cho tam giác ABC có AB =AC. Gọi M là trung điểm của BC. chứng minh :

AM là đường trung trực của BC.
kẽ đường phân giác Ax của góc ngoài A. chứng minh : Ax // BC

Giải.

Xét ΔAMB và ΔAMC, ta có :

AB =AC (gt)

MB = MC (M là trung điểm của BC)

AM cạnh chung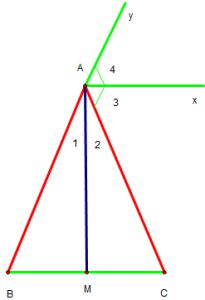

=> ΔAMB = ΔAMC (c – c – c)

=> $\widehat{AMB} =\widehat{AMC}$

Mà : $\widehat{AMB} \widehat{AMC} =180^0$ (hai góc kề bù)

=> $\widehat{AMB} =\widehat{AMC}=90^0$

Hay AM $\bot$ BC tại M.

mà : M là trung điểm của BC (gt)

vậy : AM là đường trung trực của BC

2. Ax // BC

ta có : $\widehat{A_1} =\widehat{A_2}$ (góc tương ứng của ΔAMB = ΔAMC)

=>AM đường phân giác của góc A.

=> $\widehat{A_2} =\widehat{BAC}:2$

mà : $\widehat{A_3} =\widehat{CAy}:2$ (đường phân giác Ax của góc ngoài A )

nên : $\widehat{A_2} \widehat{A_3}=\widehat{BAC}:2 \widehat{CAy}:2$

mà : $\widehat{BAC} \widehat{CAy}=180^0$

=> $\widehat{A_2} \widehat{A_3}=180^0:2=90^0$

hay : AM $\bot$ Ax.

mà :AM $\bot$ BC (cmt)

vậy : Ax // BC.

Bài 4: Cho tam giác ABC. Kẻ AH vuông góc với BC tại H trên nửa mặt phẳng BCA không chứa điểm B. Vẽ tam giác ACD sao cho AD = BC , CD = AB . Chứng minh:
a, AB // CD
b, AH vuông góc với AD

Giải.

a) cm : AB // DC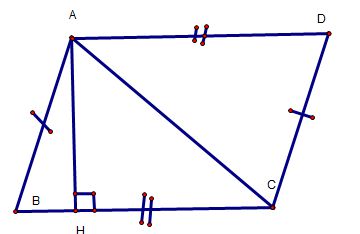
Xét ΔABC và ΔCDA , ta có :
AB = CD(gt)
BC = AD (gt)
AC cạnh chung.
=> ΔABC = ΔCDA (c – c – c)
=> $\widehat{BAC} =\widehat{ACD}$ (góc tương ứng)
=> AB // DC ( $\widehat{BAC} ; \widehat{ACD}$ so lo trong)
b) AH vuông góc với AD
Ta có :
cmtt, ta được : AD // BC
mà : AH ⊥ BC (gt)
=> AH ⊥ AD