Cách chứng minh đường thẳng là tiếp tuyến của đường tròn

Để chứng minh một đường thẳng là tiếp tuyến của một đường tròn các em hãy sử dụng định nghĩa và tính chất của tiếp tuyến để làm.

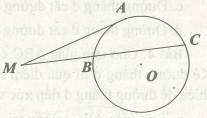
Giả sử ta cần chứng minh đường thẳng (d) là tiếp tuyến của đường tròn (O) tại tiếp điểm A. Ta có:

Phương pháp chứng minh đường thẳng là tiếp tuyến của đường tròn

– Cách 1: Chứng minh đường thẳng d vuông góc với bán kính của đường tròn. (sử dụng các phương pháp chứng minh 2 đường thẳng vuông góc trong mặt phẳng)

– Cách 2: Chứng minh khoảng cách từ tâm O của đường tròn đến đường thẳng d bằng bán kính R của đường tròn.

– Cách 3: Chứng minh hệ thức MA² = MB.MC thì MA là tiếp tuyến của đường tròn ngoại tiếp tam giác ABC.

Ví dụ chứng minh đường thẳng là tiếp tuyến của đường tròn

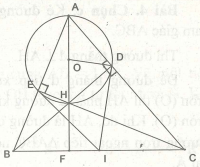
Ví dụ 1. Cho tam giác ABC nhọn, đường cao BD và CE cắt nhai tại H. Gọi I là trung điểm của BC. Chứng minh rằng ID, IE là tiếp tuyến của đường tròn ngoại tiếp tam giác ADE.

Giải

Gọi O là trung điểm của AH.

Tam giác ADH vuông tại D có DO là trung tuyến nên ta có:

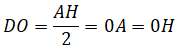
Tam giác AEH vuông tại E và có EO là trung tuyến nên ta có:

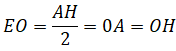
Suy ra: OA = OD = OE, do đó O là tâm đường tròn ngoại tiếp tam giác ADE.

Ta có:

(tam giác OAD cân tại O)

Tam giác BDC vuông tại D có DI là trung tuyến nên:

Suy ra: tam giác ICD cân tại I

Do đó:

H là giao điểm hai đường cao BD và CE nên là trực tâm của tam giác ABC, suy ra AH ⊥ BC tại F.

Khi đó:

Từ (1), (2) và (3) ta có:

Ta có: OD ⊥ DI, D thuộc đường tròn (O) nên ID tiếp xúc với (O) tại D.

Chứng minh tương tự ta có IE tiếp xúc với (O) tại E.

Ví dụ 2. Cho đường tròn (O) đường kính AB. Ax, By là 2 tia tiếp tuyến của (O) (Ax, By cùng nửa mặt phẳng bờ là đường thẳng AB). Trên Ax lấy điểm C, trên By lấy điểm D sao cho góc COD bằng 90º. Chứng minh rằng: CD tiếp xúc với đường tròn (O).

Giải

Gọi H là chân đường vuông góc hạ từ O xuống CD.

Ta chứng minh OH = OB = R (O)

Tia CO cắt tia đối của tia By tại E.

Xét △OAC và △OBE có:

OA =OB (=R)

Nên: △OAC = △OBF (g.c.g) ⇒ OC = OE

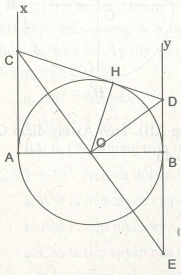
Tam giác DEC có DO vừa là đường cao vừa là trung tuyến nên là tam giác cân. Khi đó DO cũng là đường phân giác.

Ta có: OH ⊥ CD, OH = OB = R (O) nên CD tiếp xúc với (O) tại H.

Ví dụ 3. Cho đường tròn tâm O đường kính AB. Một nửa đường thẳng qua A cắt đường kính CD vuông góc với AB tại M và cắt (O) tại N.

a. Chứng minh AM.AN = AC²

b. Chứng minh đường tròn ngoại tiếp tam giác CMN tiếp xúc với AC tại C.

Giải

a. Tứ giác OBNM có góc O bằng góc N bằng 90º nên nội tiếp đường tròn.

BO và MN là hai dây của đường tròn đó cắt nhau tại A.

Do đó: AM.AN = AO.AB               (1)

Mặt khác: △ACB vuông tại C có CO là đường cao

Nên:  AC2 = AO.AB     (2)

Từ (1) và (2) suy ra AM. AN = AC².

b. Giả sử đường tròn ngoại tiếp △CMN cắt AC tại C’.

Ta có: AC.AC’ = AM.AN

Theo câu a ta có: AM.AN = AC²

Nên AC. AC’ = AC²

⇒ AC’ = AC ⇒ C’ trùng với C.

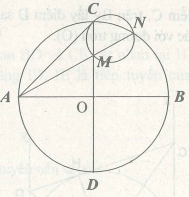
Chứng tỏ AC chỉ cắt đường tròn ngoại tiếp △CMN tại một điểm duy nhất là C.

Vậy AC là tiếp tuyến của đường tròn ngoại tiếp △CMN.

Bài tập trắc nghiệm chứng minh đường thẳng là tiếp tuyến của đường tròn có lời giải

Bài 1. Cho nửa đường tròn tâm O đường kính AB. Ax, By là hai tiếp tuyến của (O) (Ax, By cùng phía đối với đường thẳng AB). Trên Ax lấy điểm C, trên By lấy điểm D sao cho

Khi đó:

a. CD tiếp xúc với đường tròn (O)

b. CD cắt đường tròn (O)

c. CD không có điểm chung với (O)

d. CD = R²

Giải:

Chọn a.

Vì: Trên tia đổi của tia BD lấy điểm E sao cho BE = AC.

Ta có:

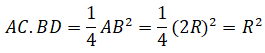
Mà AC = BE ⇒ BE.BD = 

⇒ △DOE vuông tại O

⇒ OD vừa là đường cao vừa là đường trung tuyến của △CDE nên OD cũng là đường phân giác.

⇒ △OHD = △OBD (tam giác vuông có cạnh huyền và một góc nhọn bằng nhau)

⇒ OH = OB ⇒ CD tiếp xúc với đường tròn (O).

Bài 2. Cho tam giác ABC cân tại A, đường cao AH và BK cắt nhau ở I. Khi đó:

a. AK là tiếp tuyến của đường tròn đường kính AI

b. BK là tiếp tuyến của đường tròn đường kính AI

c. BH là tiếp tuyến của đường tròn đường kính AI

d. HK là tiếp tuyến của đường tròn đường kính AI

Giải:

Chọn d.

Vì, gọi O là trung điểm của AI thì KO là đường trung tuyến của tam giác vuông AKO.

⇒ AO = IO = OK.

Ta cần chứng minh OK ⊥ HK, dựa vào tính chất △AOK cân. Từ đó suy ra rằng HK là tiếp tuyến của đường tròn đường kính AI.

Bài 3. Cho đường tròn (O) đường kính AB, lấy điểm M sao cho A nằm giữa B và M. Kẻ đường thẳng MC tiếp xúc với đường tròn (O) tại C. Từ O hạ đường thẳng vuông góc với CB và cắt tia MC tại N. Khẳng định nào sau đây không đúng?

a. BN là tiếp tuyến của đường tròn (O)

b. BC là tiếp tuyến của đường tròn (O, OH)

c. OC là tiếp tuyến của đường tròn (O, ON)

d. AC là tiếp tuyến của đường tròn (C, BC)

Giải:

Chọn b.

Vì góc OCN bằng 90º nên ba điểm O, C, N cùng thuộc đường tròn đường kính ON. Do đó OC là một dây cung, không thể là tiếp tuyến của đường tròn đường kính ON.

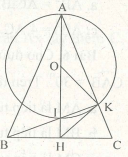
Bài 4. Cho tam giác ABC vuông tại A, đường cao AH. Đường tròn tâm I đường kính AH cắt AB tại E, đường tròn tâm J đường kính HC cắt AC tại F. Khi đó:

a. EF là tiếp tuyến của đường tròn (H, HI)

b. JF là tiếp tuyến của đường tròn (I, $\displaystyle \frac{{EF}}{2}$)

c. EF là tiếp tuyến chung của hai đường tròn (I) và (J).

d. IF là tiếp tuyến của đường tròn (C, CF).

Giải:

Chọn b.

Vì tứ giác AEHK có:

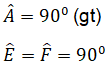
Nên AEHK là hình chữ nhật

⇒ EF cắt AH tại trung điểm I của AH

⇒ EF là đường kính của đường tròn (I)

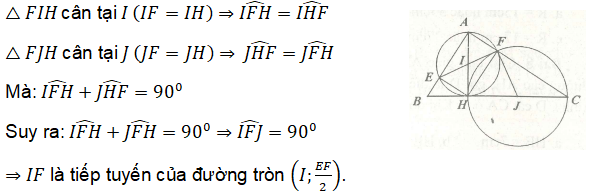
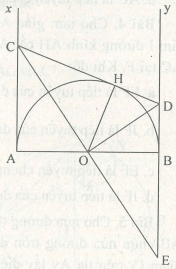
Bài 5. Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn dựng hai tiếp tuyến Ax và By. Trên tia Ax lấy điểm C, trên tia Ay lấy điểm D. Điều kiện cần và đủ để CD tiếp xúc với đường tròn (O) là:

a. AB² = AC.BD

b. AB² = 2.AC.BD

c. AB² = 4.AC.BD

d. AB² =  AC² + BD²

Giải:

Chọn c.

Bài 6. Cho đường tròn (O, R) đường kính AB. Vẽ dây cung AC sao cho góc CAB bằng 30º. Trên tia đối của tia BA lấy điểm M sao cho BM = R. Khi đó:

a. AM là tiếp tuyến của đường tròn (O).

b. BM là tiếp tuyến của đường tròn (O).

c. CM là tiếp tuyến của đường tròn (O).

d. AB là tiếp tuyến của đường tròn (O).

Giải:

Chọn c.

Bài 7. Cho hình vuông ABCD. Một đường tròn tâm O tiếp xúc với các đường thẳng AB, AD và cắt mỗi cạnh BC, CD thanh hai đoạn có độ dài 2cm và 23cm. Bán kính R của đường tròn có độ dài bằng:

a. R = 15cm hoặc 35cm

b. R = 16cm hoặc 36cm

c. R = 17cm hoặc 37cm

d. R = 18cm hoặc 38cm

Giải:

Chọn a.

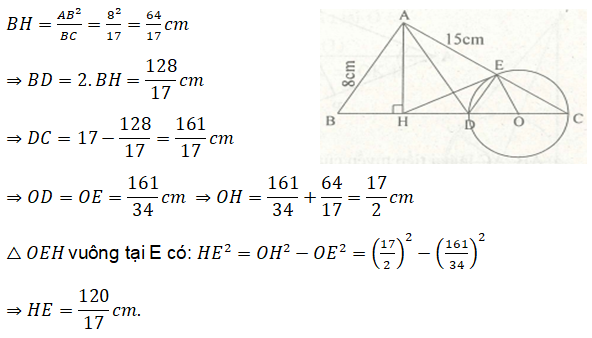
Bài 8. Cho tam giác ABC vuông ở A có AB = 8cm; AC = 15cm. Vẽ đường cao AH, gọi D là điểm đối xứng với B qua H. Vẽ đường tròn đường kính CD cắt CA ở E. Khi đó, độ dài đoạn thẳng HE bằng:

a. HE = 7cm

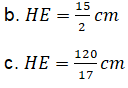
d. HE = 8cm

Giải:

Chọn c.

Vì chứng minh HE là tiếp tuyến của đường tròn (O)

Ta có: BC² =  AB² + AC² = 8² + 15² = 289 cm

⇒ BC = 17cm

• Chuyên đề: Phương trình trùng phương

• 8 cách chứng minh tia Oz là tia phân giác của góc xÔy

• Chủ đề 4: Đồ thị hàm số – Phần Đại số

• Mở rộng một số bất đẳng thức

• Chứng minh bất đẳng thức bằng phương pháp phản chứng

• 4 phương pháp giải phương trình vô tỷ – Trung tâm Gia sư Hà Nội

• Các dạng toán Đại số thường gặp trong đề thi vào 10