Ứng dụng vectơ để chứng minh hai đường thẳng song song, 3 đường thẳng đồng quy – Toán lớp 10

1. PHƯƠNG PHÁP GIẢI

Để chứng minh đường thẳng $A B$ song song với $C D$ ta đi chứng minh $\vec{A B} = k \vec{C D}$ và điểm $A$ không thuộc đường thẳng $C D .$
Để chứng minh ba đường thẳng đồng quy ta có thể chứng minh theo hai hướng sau:
+ Chứng minh mỗi đường thẳng cùng đi qua một điểm cố định.
+ Chứng minh một đường thẳng đi qua giao điểm của hai đường thẳng còn lại.

2. CÁC VÍ DỤ

Ví dụ 1: Cho ngũ giác $A B C D E .$ Gọi $M$ , $N$ , $P$ , $Q$ lần lượt là trung điểm của các cạnh $A B$ , $B C$ , $C D$ , $D E .$ Gọi $I$ , $J$ lần lượt là trung điểm của các đoạn $M P$ và $N Q .$ Chứng minh rằng $I J$ song song với $A E .$

Ứng dụng vectơ để chứng minh 3 điểm thẳng hàng, đi qua điểm cố định - Toán lớp 10

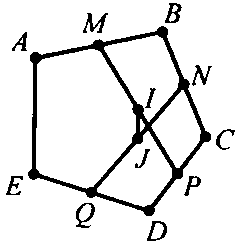
Ta có: $2 \vec{I J} = \vec{I Q} + \vec{I N}$ $= \vec{I M} + \vec{M Q} + \vec{I P} + \vec{P N} .$
$= \vec{M Q} + \vec{P N}$ $= \frac{1}{2} (\vec{A E} + \vec{B D}) + \frac{1}{2} \vec{D B}$ $= \frac{1}{2} \vec{A E} .$
Suy ra $I J$ song song với $A E .$

Ví dụ 2: Cho tam giác $A B C .$ Các điểm $M$ , $N$ , $P$ thuộc các đường thẳng $B C$ , $C A$ , $A B$ thỏa mãn $α + β + γ \neq 0$ , $β \vec{M B} + γ \vec{M C}$ $= γ \vec{N C} + α \vec{N A}$ $= α \vec{P A} + β \vec{P B} = \vec{0}$ thì $A M$ , $B N$ , $C P$ đồng quy tại $O$ , với $O$ là điểm được xác định bởi $α \vec{O A} + β \vec{O B} + γ \vec{O C} = \vec{0} .$

Ta có $β \vec{M B} + γ \vec{M C} = \vec{0}$ $\Leftrightarrow β (\vec{M O} + \vec{O B})$ $+ γ (\vec{M O} + \vec{O C}) = \vec{0} .$
$\Leftrightarrow α \vec{O A} + β \vec{O B} + γ \vec{O C}$ $+ (β + γ) \vec{M O} = α \vec{O A} .$
$\Leftrightarrow (β + γ) \vec{M O} = α \vec{O A} .$
Suy ra $M$ , $O$ , $A$ thẳng hàng hay $A M$ đi qua điểm cố định $O .$
Tương tự ta có $B N$ , $C P$ đi qua $O .$
Vậy ba đường thẳng $A M$ , $B N$ , $C P$ đồng quy.

Ví dụ 3: Cho sáu điểm trong đó không có ba điểm nào thẳng hàng. Gọi $Δ$ là một tam giác có ba đỉnh lấy trong sáu điểm đó và $Δ^{'}$ là tam giác có ba đỉnh còn lại. Chứng minh rằng với các cách chọn $Δ$ khác nhau, các đường thẳng nối trọng tâm hai tam giác $Δ$ và $Δ^{'}$ đồng quy.

Định hướng: Giả sử sáu điểm đó là $A$ , $B$ , $C$ , $D$ , $E$ , $F .$
Ta cần chứng minh tồn tại một điểm $H$ cố định sao cho với các cách chọn $Δ$ khác nhau thì $H$ thuộc các đường thẳng nối trọng tâm hai tam giác $Δ$ và $Δ^{'}$ . Nếu $Δ$ là tam giác $A B C$ thì $Δ$ là tam giác $D E F .$ Gọi $G$ và $G^{'}$ lần lượt là trọng tâm của tam giác $A B C$ và tam giác $D E F .$
$H$ thuộc đường thẳng $G G^{'}$ khi có số thực $k$ sao cho $\vec{H G} = k \vec{H G^{'}} .$
$\Leftrightarrow \frac{1}{3} (\vec{H A} + \vec{H B} + \vec{H C})$ $= \frac{k}{3} (\vec{H D} + \vec{H E} + \vec{H F}) .$
$\Leftrightarrow \frac{1}{3} \vec{H A} + \frac{1}{3} \vec{H B} + \frac{1}{3} \vec{H C}$ $- \frac{k}{3} \vec{H D} - \frac{k}{3} \vec{H E} - \frac{k}{3} \vec{H F} = \vec{0} .$
Vì vai trò của các điểm $A$ , $B$ , $C$ , $D$ , $E$ , $F$ trong bài toán bình đẳng nên chọn $k$ sao cho $- \frac{k}{3} = \frac{1}{3} \Leftrightarrow k = - 1$ khi đó $\vec{H A} + \vec{H B} + \vec{H C} + \vec{H D} + \vec{H E} + \vec{H F} = \vec{0} .$
Lời giải: Gọi $H$ là trọng tâm sáu điểm $A$ , $B$ , $C$ , $D$ , $E$ , $F$ khi đó:
$\vec{H A} + \vec{H B} + \vec{H C} + \vec{H D} + \vec{H E} + \vec{H F} = \vec{0}$ $(*) .$
Giả sử $G$ , $G^{'}$ lần lượt là trọng tâm của hai tam giác $A B C$ , $D E F$ suy ra:
$\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$ , $\vec{G^{'} D} + \vec{G^{'} E} + \vec{G^{'} F} = \vec{0} .$
Suy ra: $(*) \Leftrightarrow 3 \vec{H G} + \vec{G A} + \vec{G B} + \vec{G C}$ $= 3 \vec{H G^{'}} + \vec{G^{'} D} + \vec{G^{'} E} + \vec{G^{'} F} .$
$\Leftrightarrow \vec{H G} = \vec{H G^{'}}$
Do đó $G G^{'}$ đi qua điểm cố định $H$ , do đó các đường thẳng nối trọng tâm hai tam giác $Δ$ và $Δ^{'}$ đồng quy.

3. BÀI TẬP LUYỆN TẬP

Bài 1: Cho tứ giác $A B C D$ , gọi $K$ , $L$ lần lượt là trọng tâm của các tam giác $A B C$ và tam giác $B C D .$ Chứng minh rằng hai đường thẳng $K L$ và $A D$ song song với nhau.

Ta có $\vec{K A} + \vec{K B} + \vec{K C} = \vec{0}$ và $\vec{L B} + \vec{L C} + \vec{L D} = \vec{0} .$
Trừ vế với vế ta được:
$\vec{K A} - \vec{L D} + 2 \vec{K L} = \vec{0}$ $\Leftrightarrow (\vec{K L} + \vec{L A}) - \vec{L D} + 2 \vec{K L} = \vec{0}$ $\Leftrightarrow \vec{D A} + 3 \vec{K L} = \vec{0} .$
Suy ra $K L / / A D .$

Bài 2: Trên các cạnh $B C$ , $C A$ , $A B$ của tam giác $A B C$ lần lượt lấy các điểm $A_{1}$ , $B_{1}$ , $C_{1}$ sao cho $\frac{A_{1} B}{A_{1} C} = \frac{B_{1} C}{B_{1} A} = \frac{C_{1} A}{C_{1} B} = k$ $(k > 0) .$ Trên các cạnh $B_{1} C_{1}$ , $C_{1} A_{1}$ , $A_{1} B_{1}$ lần lượt lấy các điểm $A_{2}$ , $B_{2}$ , $C_{2}$ sao cho $\frac{A_{2} B_{1}}{A_{2} C_{1}} = \frac{B_{2} C_{1}}{B_{2} A_{1}} = \frac{C_{2} A_{1}}{C_{2} B_{1}} = \frac{1}{k} .$ Chứng minh rằng tam giác $A_{2} B_{2} C_{2}$ có các cạnh tương ứng song song với các cạnh của tam giác $A B C .$

$\vec{A_{2} C_{2}} = \frac{k^{2} - k + 1}{{(k + 1)}^{2}} \vec{A C}$ , vì $k^{2} - k + 1 > 0$ và $A_{2} \notin A C$ nên $A_{2} C_{2} / / A C .$
Tương tự ta có $B_{2} C_{2} / / B C$ và $A_{2} B_{2} / / A B .$

Bài 3: Trên đường tròn cho năm điểm trong đó không có ba điểm nào thẳng hàng. Qua trọng tâm của ba trong năm điểm đó kẻ đường thẳng vuông góc với đường thẳng đi qua hai điểm còn lại. Chứng minh rằng mười đường thẳng nhận được cắt nhau tại một điểm.

Giả sử năm điểm đó là $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ , $A_{5}$ nằm trên đường tròn $(O) .$ Ta cần chứng minh tồn tại điểm $H$ thuộc mười đường thẳng đó.
Gọi $G$ là trọng tâm của tam giác $A_{1} A_{2} A_{3}$ , $P$ là trung điểm của đoạn thẳng $A_{4} A_{5} .$ Vì $O P ⊥ A_{4} A_{5}$ (do $O A_{4} = O A_{5}$ ) nên điểm $H$ thuộc đường thẳng đi qua $G$ và vuông góc với đường thẳng $A_{4} A_{5}$ khi có số thực $k$ sao cho $\vec{H G} = k \vec{O P} .$ Mà $\vec{O G} = \frac{1}{3} (\vec{O A_{1}} + \vec{O A_{2}} + \vec{O A_{3}})$ (vì $G$ là trọng tâm của tam giác $A_{1} A_{2} A_{3}$ ). $\vec{O P} = \frac{1}{2} (\vec{O A_{4}} + \vec{O A_{5}})$ (vì $P$ là trung điểm của đoạn thẳng $A_{4} A_{5}$ ).
Do đó $\vec{H G} = k \vec{O P}$ $\Leftrightarrow \vec{O G} - \vec{O H} = k \vec{O P} .$
Hay $\frac{1}{3} (\vec{O A_{1}} + \vec{O A_{2}} + \vec{O A_{3}}) - \vec{O H}$ $= \frac{k}{2} (\vec{O A_{4}} + \vec{O A_{5}}) .$
$\Leftrightarrow \vec{O H} = \frac{1}{3} \vec{O A_{1}} + \frac{1}{3} \vec{O A_{2}}$ $+ \frac{1}{3} \vec{O A_{3}} - \frac{k}{2} \vec{O A_{4}} - \frac{k}{2} \vec{O A_{5}} .$
Vì các điểm $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ , $A_{5}$ trong bài toán có vai trò bình đẳng nên chọn $k$ sao cho $- \frac{k}{2} = \frac{1}{3} \Leftrightarrow k = - \frac{2}{3} .$
Khi đó $\vec{O H} = \frac{1}{3} (\vec{O A_{1}} + \vec{O A_{2}} + \vec{O A_{3}} + \vec{O A_{4}} + \vec{O A_{5}}) .$
Hay $\vec{O H} = \frac{5}{3} \vec{O G}$ ( $G$ là trọng tâm của hệ điểm ${A_{1}, A_{2}, A_{3}, A_{4}, A_{5}}$ ).

Bài 4: Cho tứ giác $A B C D$ nội tiếp đường tròn $(O) .$ Gọi $M$ , $N$ , $P$ , $Q$ lần lượt là trung điểm của các cạnh $A B$ , $B C$ , $C D$ , $D A .$ Kẻ $M M^{'}$ , $N N^{'}$ , $P P^{'}$ , $Q Q^{'}$ lần lượt vuông góc với $C D$ , $D A$ , $A B$ , $B C .$ Chứng tỏ rằng bốn đường thẳng $M M^{'}$ , $N N^{'}$ , $P P^{'}$ , $Q Q^{'}$ đồng quy tại một điểm. Nhận xét về điểm đồng quy và hai điểm $I$ , $O$ ( $I$ là giao điểm của $M P$ và $N Q$ ).

Ta cần chứng minh tồn tại điểm $H$ thuộc đường thẳng $M M^{'}$ , $N N^{'}$ , $P P^{'}$ , $Q Q^{'} .$
Vì $O P ⊥ C D$ (do $O C = O D$ ) nên điểm $H$ thuộc đường thẳng $M M^{'}$ khi có số thực $k$ sao cho $\vec{H M} = k \vec{O P} .$
Mà $M$ và $P$ lần lượt là trung điểm của $A B$ và $C D$ nên:
$\vec{H M} = \frac{1}{2} (\vec{H A} + \vec{H B})$ , $\vec{O P} = \frac{1}{2} (\vec{O C} + \vec{O D}) .$
Do đó $\vec{H M} = k \vec{O P}$ hay $\frac{1}{2} (\vec{H A} + \vec{H B}) = \frac{k}{2} (\vec{O C} + \vec{O D}) .$
$\Leftrightarrow \vec{H O} + \vec{O A} + \vec{H O} + \vec{O B}$ $= k (\vec{O C} + \vec{O D})$ $\Leftrightarrow 2 \vec{O H} = \vec{O A} + \vec{O B} - k \vec{O C} - k \vec{O D} .$
Vì các điểm $A$ , $B$ , $C$ , $D$ trong bài toán có vai trò bình đẳng nên chọn $k = - 1.$
Khi đó $2 \vec{O H} = \vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} .$
Hay $2 \vec{O H} = 4 \vec{O I}$ (dễ thấy $I$ là trọng tâm của tứ giác $A B C D$ ) $\Leftrightarrow \vec{O H} = 2 \vec{O I} .$
Vậy $H$ là điểm đối xứng của $O$ qua $I .$

Bài 5: Cho năm điểm trong đó không có ba điểm nào thẳng hàng. Gọi $Δ$ là một tam giác có ba đỉnh lấy trong năm điểm đó, hai điểm còn lại xác định một đoạn thẳng $θ .$ Chứng minh rằng với các cách chọn $Δ$ khác nhau, các đường thẳng nối trọng tâm tam giác $Δ$ và trung điểm đoạn thẳng $θ$ luôn đi qua một điểm cố định.

Gọi $A$ , $B$ , $C$ là ba đỉnh của tam giác $Δ$ và $D E$ là đoạn thẳng $θ .$ Gọi $G$ là trọng tâm tam giác $Δ$ và $M$ là trung điểm của $D E$ , thì với điểm $O$ tùy ý ta có: $\vec{O A} + \vec{O B} + \vec{O C} + \vec{O D} + \vec{O E}$ $= 3 \vec{O G} + 2 \vec{I M} .$
Do đó $G M$ luôn đi qua điểm cố định $O$ là trọng tâm hệ điểm $A$ , $B$ , $C$ , $D$ , $E .$

Bài 6: Cho tam giác $A B C .$ Ba đường thẳng $x$ , $y$ , $z$ lần lượt đi qua $A$ , $B$ , $C$ và chúng chia đôi chu vi tam giác $A B C .$ Chứng minh rằng $x$ , $y$ , $z$ đồng quy.

Đặt $B C = a$ , $C A = b$ , $A B = c .$
Giả sử đường thẳng $x$ đi qua $A$ cắt $B C$ tại $M$ khi đó ta có:
$A B + B M = A C + M C$ $\Leftrightarrow c + B M = b + M C$ $\Rightarrow c + 2 B M = b + (B M + M C) .$
Suy ra $B M = \frac{a + b - c}{2}$ , $C M = \frac{a - b + c}{2} .$
Do đó: $(a + c - b) \vec{M B} + (a + b - c) \vec{M C} = \vec{0} .$
Tương tự ta có:
$(a + b - c) \vec{N C} + (b + c - a) \vec{N A}$ $= (b + c - a) \vec{P A} + (a + c - b) \vec{P B} = \vec{0} .$
Do đó $x$ , $y$ , $z$ đồng quy tại $I$ được xác định bởi:
$(b + c - a) \vec{I A}$ $+ (a + c - b) \vec{I B}$ $+ (a + b - c) \vec{I C} = \vec{0} .$

Bài 7: Cho tam giác $A B C$ , các đường tròn bàng tiếp góc $A$ , $B$ , $C$ tương ứng tiếp xúc với các cạnh $B C$ , $C A$ , $A B$ tại $M$ , $N$ , $P .$ Chứng minh $A M$ , $B N$ , $C P$ cùng đi qua một điểm, xác định điểm đó.

Giả sử đường tròn bàng tiếp góc $A$ tiếp xúc $B C$ tại $M .$
Gọi $B^{'}$ , $C^{'}$ là tiếp điểm của cạnh $A B$ , $A C$ với đường tròn bàng tiếp góc $A .$
Khi đó $A B^{'} = A C^{'}$ $\Leftrightarrow A B + B B^{'} = A C + C C^{'}$ $\Leftrightarrow c + B M = c + C M .$
Bạn đọc tự giải tiếp.

Bài 8: Cho tứ giác $A B C D .$ Gọi $M$ , $N$ , $P$ , $Q$ là trung điểm các cạnh $A B$ , $B C$ , $C D$ , $D A .$
a) Gọi $G$ là giao điểm của $M P$ và $N Q .$ Chứng minh rằng $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D} = \vec{0} .$
b) Gọi $A_{1}$ , $B_{1}$ , $C_{1}$ , $D_{1}$ lần lượt là trọng tâm các tam giác $B C D$ , $C D A$ , $D A B$ , $A B C .$ Chứng minh rằng các đường thẳng $A A_{1}$ , $B B_{1}$ , $C C_{1}$ , $D D_{1}$ đồng quy tại điểm $G .$

a) Ta có: $\vec{G A} + \vec{G B} + \vec{G C} + \vec{G D}$ $= 2 \vec{G M} + \vec{M A} + \vec{M B} + 2 \vec{G P} + \vec{P C} + \vec{P D}$ $= 2 (\vec{G M} + \vec{G P})$ $+ (\vec{M A} + \vec{M B})$ $+ (\vec{P C} + \vec{P D}) = \vec{0} .$
b) $3 \vec{A A_{1}} = \vec{A B} + \vec{A C} + \vec{A D}$ , $4 \vec{A G} = \vec{A B} + \vec{A C} + \vec{A D}$ $\Rightarrow \vec{A A_{1}} = \frac{4}{3} \vec{A G} .$
$\Rightarrow \vec{A A_{1}}$ , $\vec{A G}$ cùng phương hay $A A_{1}$ đi qua $G .$
Tương tự ta có $B B_{1}$ đi qua $G$ , $C C_{1}$ đi qua $G$ , $D D_{1}$ đi qua $G .$
Vậy ta có $A A_{1}$ , $B B_{1}$ , $C C_{1}$ , $D D_{1}$ đồng quy tại $G .$

Bài 9: Cho tam giác $A B C$ có trọng tâm $G$ , $M$ là một điểm tùy ý. Gọi $A_{1}$ , $B_{1}$ , $C_{1}$ lần lượt là các điểm đối xứng với $M$ qua các trung điểm $I$ , $J$ , $K$ của các cạnh $B C$ , $C A$ , $A B .$ Chứng minh rằng:
a) Các đường thẳng $A A_{1}$ , $B B_{1}$ , $C C_{1}$ đồng quy tại trung điểm $O$ của mỗi đường.
b) $M$ , $G$ , $O$ thẳng hàng và $\frac{M O}{M G} = \frac{3}{2} .$

a) Gọi $O$ là trung điểm $C C_{1} .$
$\vec{A A_{1}} = \vec{A M} + \vec{M A_{1}}$ $= \vec{A M} + \vec{M B} + \vec{M C}$ $= \vec{A C} + \vec{M B} .$
$2 \vec{A O} = \vec{A C} + \vec{A C_{1}}$ $= \vec{A C} + \vec{M B}$ (vì $A C_{1} B M$ hình bình hành).
$\Rightarrow \vec{A A_{1}} = 2 \vec{A O}$ hay $O$ là trung điểm $A A_{1} .$
Tương tự ta có $\vec{B B_{1}} = 2 \vec{B O}$ hay $O$ là trung điểm $B B_{1} .$
Vậy $A A_{1}$ , $B B_{1}$ , $C C_{1}$ đồng quy tại trung điểm $O$ của mỗi đường.
b) Ta có: $3 \vec{M G} = \vec{M A} + \vec{M B} + \vec{M C} .$
$2 \vec{M O} = \vec{M A} + \vec{M A_{1}}$ $= \vec{M A} + \vec{M B} + \vec{M C}$ $\Rightarrow 2 \vec{M O} = 3 \vec{M G} .$
$\Rightarrow M$ , $G$ , $O$ thẳng hàng và $\frac{M O}{M G} = \frac{3}{2} .$

Bài 10: Cho tam giác $A B C .$ Gọi $M$ , $N$ , $P$ là các tiếp điểm của đường tròn nội tiếp tam giác $A B C$ với các cạnh $B C$ , $C A$ , $A B .$ Gọi $Δ_{a}$ là đường thẳng đi qua trung điểm $P N$ và vuông góc với $B C$ , $Δ_{b}$ là đường thẳng đi qua trung điểm $P M$ và vuông góc với $A C$ , $Δ_{c}$ là đường thẳng đi qua trung điểm $M N$ và vuông góc với $A B .$ Chứng minh rằng $Δ_{a}$ , $Δ_{b}$ và $Δ_{c}$ đồng quy.

Đặt $\vec{I M} = \vec{e_{1}}$ , $\vec{I N} = \vec{e_{2}}$ , $\vec{I P} = \vec{e_{3}} .$
Gọi $X$ , $Y$ , $Z$ lần lượt là trung điểm của $N P$ , $P M$ , $M N .$
$O$ là điểm được xác định $2 \vec{I O} = \vec{e_{1}} + \vec{e_{2}} + \vec{e_{3}} .$
Suy ra $\vec{O X} = \vec{O I} + \vec{I X}$ $= - \frac{1}{2} (\vec{e_{1}} + \vec{e_{2}} + \vec{e_{3}})$ $+ \frac{1}{2} (\vec{e_{2}} + \vec{e_{3}})$ $= - \frac{1}{2} \vec{e_{1}} .$
Suy ra $O X ⊥ B C$ , tương tự ta có $O Y ⊥ A C$ , $O Z ⊥ A B .$
Suy ra $Δ_{a}$ , $Δ_{b}$ và $Δ_{c}$ đồng quy tại $O .$

Bài 11: Cho hai hình bình hành $A B C D$ và $A B^{'} C^{'} D^{'}$ sắp xếp sao cho $B^{'}$ thuộc cạnh $A B$ , $D^{'}$ thuộc cạnh $A D .$ Chứng minh rằng các đường thẳng $D B^{'}$ , $C C^{'}$ , $B D^{'}$ đồng quy.

Đặt $\frac{A B^{'}}{A B} = m$ , $\frac{A D^{'}}{A D} = n$ $(0 < m, n < 1) .$
Gọi $I$ là giao điểm $B D^{'}$ và $D B^{'} .$
Ta có $\vec{A C} = \vec{A B} + \vec{A D}$ , $\vec{A C^{'}} = \vec{A B^{'}} + \vec{A D^{'}}$ $= m \vec{A B} + n \vec{A D} .$
$\frac{A D^{'}}{A D} = n$ $\Rightarrow \vec{D^{'} A} = \frac{n}{n - 1} \vec{D^{'} D}$ $\Rightarrow \vec{B D^{'}} = \frac{\vec{B A} - \frac{n}{n - 1} \vec{B D}}{1 - \frac{n}{n - 1}}$ $= \frac{1 - n}{1 - m} \vec{B B^{'}} + n \vec{B D} .$
$\Rightarrow \frac{1 - n}{1 - m} \vec{I B^{'}} + n \vec{I D} = \vec{0}$ $\Rightarrow \vec{I B^{'}} = \frac{n (m - 1)}{1 - n} \vec{I D} .$
$\Rightarrow \vec{A I} = \frac{\vec{A B^{'}} + \frac{n (m - 1)}{n - 1} \vec{A D}}{1 + \frac{n (m - 1)}{n - 1}}$ $= \frac{m (n - 1) \vec{A B} + n (m - 1) \vec{A D}}{m n - 1} .$
Do đó $\vec{I C} = \vec{A C} - \vec{A I}$ $= \frac{1}{m n - 1} ((m - 1) \vec{A B} + (n - 1) \vec{A D}) .$
$\vec{C^{'} C} = \vec{A C} - \vec{A C^{'}}$ $= (1 - m) \vec{A B} + (1 - n) \vec{A D} .$
Suy ra $\vec{I C} = \frac{1}{m n - 1} \vec{C^{'} C} .$
Suy ra $I$ , $C^{'}$ , $C$ thẳng hàng, suy ra điều phải chứng minh.

Toán lớp 10 - Tags: đồng quy, đường thẳng, song song, vectơ

Ứng dụng vectơ để chứng minh hai đường thẳng song song, 3 đường thẳng đồng quy – Toán lớp 10

1. PHƯƠNG PHÁP GIẢI

2. CÁC VÍ DỤ

3. BÀI TẬP LUYỆN TẬP

Cách chứng minh đẳng thức véctơ – Toán lớp 10

Đề cương ôn tập HK2 môn Toán lớp 10

244 câu trắc nghiệm Đại số lớp 10 chương 3 có lời giải

Chuyên đề Hàm số lượng giác – Toán lớp 10

Phương pháp giải toán hình học trên tọa độ Oxy lớp 10

Bài tập trắc nghiệm Số gần đúng và Sai số – Đại số 10

Bài tập trắc nghiệm Mệnh đề và suy luận toán học – Đại số 10