Ứng dụng vectơ để chứng minh 3 điểm thẳng hàng, đi qua điểm cố định – Toán lớp 10

1. PHƯƠNG PHÁP GIẢI

+ Để chứng minh ba điểm $A$ , $B$ , $C$ thẳng hàng ta chứng minh hai vectơ $\vec{A B}$ và $\vec{A C}$ cùng phương, tức là tồn tại số thực $k$ sao cho: $\vec{A B} = k \vec{A C} .$

+ Để chứng minh đường thẳng $A B$ đi qua điểm cố định ta đi chứng minh ba điểm $A$ , $B$ , $H$ thẳng hàng với $H$ là một điểm cố định.

2. Ví dụ chứng minh 3 điểm thẳng hàng

Ví dụ 1: Cho hai điểm phân biệt $A$ , $B .$ Chứng minh rằng $M$ thuộc đường thẳng $A B$ khi và chỉ khi có hai số thực $α$ , $β$ có tổng bằng $1$ sao cho: $\vec{O M} = α \vec{O A} + β \vec{O B} .$

Nếu $A$ , $B$ , $M$ thẳng hàng $\Rightarrow \vec{A M} = k \vec{A B}$ $\Leftrightarrow \vec{A O} + \vec{O M} = k (\vec{A O} + \vec{O B}) .$
$\Rightarrow \vec{O M} = (1 - k) \vec{O A} + k \vec{O B} .$

Đặt $α = 1 - k$ , $β = k$ $\Rightarrow α + β = 1$ và $\vec{O M} = α \vec{O A} + β \vec{O B} .$

Nếu $\vec{O M} = α \vec{O A} + β \vec{O B}$ với $α + β = 1$ $\Rightarrow β = 1 - α .$

$\Rightarrow \vec{O M} = α \vec{O A} + (1 - α) \vec{O B}$ $\Rightarrow \vec{O M} - \vec{O B} = α (\vec{O A} - \vec{O B})$ $\Rightarrow \vec{B M} = α \vec{B A} .$
Suy ra $M$ , $A$ , $B$ thẳng hàng.

Ví dụ 2: Cho góc $x O y .$ Các điểm $A$ , $B$ thay đổi lần lượt nằm trên $O x$ , $O y$ sao cho $O A + 2 O B = 3.$ Chứng minh rằng trung điểm $I$ của $A B$ thuộc một đường thẳng cố định.

Định hướng: Ta có hệ thức vectơ xác định điểm $I$ là $\vec{O I} = \frac{1}{2} \vec{O A} + \frac{1}{2} \vec{O B}$ $(*) .$

Từ ví dụ 1 ta cần xác định hai điểm cố định $A^{'}$ , $B^{'}$ sao cho $\vec{O I} = α \vec{O A^{'}} + β \vec{O B^{'}}$ với $α + β = 1.$

Do đó từ hệ thức $(*)$ ta nghĩ tới việc xác định hai điểm cố định $A^{'}$ , $B^{'}$ lần lượt trên $O x$ , $O y .$

Ta có: $(*) \Leftrightarrow \vec{O I} = \frac{O A}{2 O A^{'}} \vec{O A^{'}} + \frac{O B}{2 O B^{'}} \vec{O B^{'}} .$ Từ đó ta cần chọn các điểm đó sao cho $\frac{O A}{2 O A^{'}} + \frac{O B}{2 O B^{'}} = 1.$ Kết hợp với giả thiết $O A + 2 O B = 3$ ta chọn được điểm $A^{'}$ và $B^{'}$ sao cho $O A^{'} = \frac{3}{2}$ , $O B^{'} = \frac{3}{4} .$

Lời giải: Trên $O x$ , $O y$ lần lượt lấy hai điểm $A^{'}$ , $B^{'}$ sao cho $O A^{'} = \frac{3}{2}$ , $O B^{'} = \frac{3}{4} .$

Do $I$ là trung điểm của $A B$ nên $\vec{O I} = \frac{1}{2} \vec{O A} + \frac{1}{2} \vec{O B}$ $= \frac{O A}{2 O A^{'}} \vec{O A^{'}} + \frac{O B}{2 O B^{'}} \vec{O B^{'}} .$

Ta có: $\frac{O A}{2 O A^{'}} + \frac{O B}{2 O B^{'}}$ $= \frac{O A}{2. \frac{3}{2}} + \frac{O B}{2. \frac{3}{4}}$ $= \frac{1}{3} (O A + 2 O B) = 1.$

Do đó điểm $I$ thuộc đường thẳng $A^{'} B^{'}$ cố định.

Ví dụ 3: Cho hình bình hành $A B C D$ , $I$ là trung điểm của cạnh $B C$ và $E$ là điểm thuộc đoạn $A C$ thỏa mãn $\frac{A E}{A C} = \frac{2}{3} .$ Chứng minh ba điểm $D$ , $E$ , $I$ thẳng hàng.

Định hướng: Để chứng minh $D$ , $E$ , $I$ thẳng hàng ta đi tìm số $k$ sao cho $\vec{D E} = k \vec{D I}$ , muốn vậy ta sẽ phân tích các vectơ $\vec{D E}$ , $\vec{D I}$ qua hai vectơ không cùng phương $\vec{A B}$ và $\vec{A D}$ và sử dụng nhận xét: $m \vec{a} + n \vec{b} = \vec{0}$ $\Leftrightarrow m = n = 0$ với $\vec{a}$ , $\vec{b}$ là hai vectơ không cùng phương, từ đó tìm được $k = \frac{2}{3} .$

Ứng dụng vectơ để chứng minh 3 điểm thẳng hàng, đi qua điểm cố định - Toán lớp 10

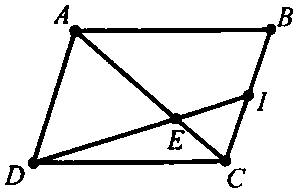
Lời giải: Ta có $\vec{D I} = \vec{D C} + \vec{C I}$ $= \vec{D C} + \frac{1}{2} \vec{C B}$ $= \vec{A B} - \frac{1}{2} \vec{A D}$ $(1) .$

Mặt khác theo giả thiết ta có $\vec{A E} = \frac{2}{3} \vec{A C}$ suy ra:

$\vec{D E} = \vec{D A} + \vec{A E}$ $= \vec{D A} + \frac{2}{3} \vec{A C}$ $= - \vec{A D} + \frac{2}{3} (\vec{A B} + \vec{A D})$

$= \frac{2}{3} \vec{A B} - \frac{1}{3} \vec{A D}$ $(2) .$

Từ $(1)$ và $(2)$ suy ra $\vec{D E} = \frac{2}{3} \vec{D I} .$

Vậy ba điểm $D$ , $E$ , $I$ thẳng hàng.

Ví dụ 4: Hai điểm $M$ , $N$ chuyển động trên hai đoạn thẳng cố định $B C$ và $B D$ $(M \neq B, N \neq B)$ sao cho $2 \frac{B C}{B M} + 3 \frac{B D}{B N} = 10.$ Chứng minh rằng đường thẳng $M N$ luôn đi qua một điểm cố định.

Dễ thấy luôn tồn tại điểm $I$ thuộc $M N$ sao cho $2 \frac{B C}{B M} \vec{I M} + 3 \frac{B D}{B N} \vec{I N} = \vec{0}$ $(1) .$

Gọi $H$ là điểm thỏa mãn $2 \vec{H C} + 3 \vec{H D} = \vec{0}$ $(2)$ , do đó $H$ cố định.

Ta có $(2) \Leftrightarrow 5 \vec{H B} + 2 \vec{B C} + 3 \vec{B D} = \vec{0} .$

$\Leftrightarrow \frac{2 B C}{B M} \vec{B M} + \frac{3 B D}{B N} \vec{B N} = 5 \vec{B H} .$

$\Leftrightarrow \frac{2 B C}{B M} (\vec{B I} + \vec{I M}) + \frac{3 B D}{B N} (\vec{B I} + \vec{I N}) = 5 \vec{B H} .$

$\Leftrightarrow (2 \frac{B C}{B M} + 3 \frac{B D}{B N}) \vec{B I} = 5 \vec{B H}$ (theo $(1)$ ).

$\Leftrightarrow 10 \vec{B I} = 5 \vec{B H}$ $\Leftrightarrow \vec{B I} = \frac{1}{2} \vec{B H}$ $(3) .$

Do các điểm $B$ , $H$ cố định, nên điểm $I$ cố định (xác định bởi hệ thức $(3)$ ).

Ví dụ 5: Cho ba dây cung song song $A A_{1}$ , $B B_{1}$ , $C C_{1}$ của đường tròn $(O) .$ Chứng minh rằng trực tâm của ba tam giác $A B C_{1}$ , $B C A_{1}$ , $C A B_{1}$ nằm trên một đường thẳng.

Gọi $H_{1}$ , $H_{2}$ , $H_{3}$ lần lượt là trực tâm của các tam giác $A B C_{1}$ , $B C A_{1}$ , $C A B_{1} .$
Ta có: $\vec{O H_{1}} = \vec{O A} + \vec{O B} + \vec{O C_{1}}$ , $\vec{O H_{2}} = \vec{O B} + \vec{O C} + \vec{O A_{1}}$ và

$\vec{O H_{3}} = \vec{O C} + \vec{O A} + \vec{O B_{1}} .$

Suy ra $\vec{H_{1} H_{2}} = \vec{O H_{2}} - \vec{O H_{1}}$ $= \vec{O C} - \vec{O C_{1}} + \vec{O A_{1}} - \vec{O A}$ $= \vec{C_{1} C} + \vec{A A_{1}} .$

$\vec{H_{1} H_{3}} = \vec{O H_{3}} - \vec{O H_{1}}$ $= \vec{O C} - \vec{O C_{1}} + \vec{O B_{1}} - \vec{O B}$ $= \vec{C_{1} C} + \vec{B B_{1}} .$

Vì các dây cung $A A_{1}$ , $B B_{1}$ , $C C_{1}$ song song với nhau.

Nên ba vectơ $\vec{A A_{1}}$ , $\vec{B B_{1}}$ , $\vec{C C_{1}}$ có cùng phương.

Do đó hai vectơ $\vec{H_{1} H_{2}}$ và $\vec{H_{1} H_{3}}$ cùng phương hay ba điểm $H_{1}$ , $H_{2}$ , $H_{3}$ thẳng hàng.

3. BÀI TẬP LUYỆN TẬP

Bài 1: Cho tam giác $A B C .$ Gọi $M$ là điểm thuộc cạnh $A B$ , $N$ là điểm thuộc cạnh $A C$ sao cho $A M = \frac{1}{3} A B$ , $A N = \frac{3}{4} A C .$ Gọi $O$ là giao điểm của $C M$ và $B N .$ Trên đường thẳng $B C$ lấy $E .$ Đặt $\vec{B E} = x \vec{B C} .$ Tìm $x$ để $A$ , $O$ , $E$ thẳng hàng.

Giải:

Ta có: $\vec{A O} = \frac{1}{9} \vec{A B} + \frac{1}{4} \vec{A C} .$ ,

$\vec{A E} = (1 - x) \vec{A B} + x \vec{A C} .$

$A$ , $E$ , $O$ thẳng hàng $\Leftrightarrow \vec{A E} = k \vec{A O} .$

$\Leftrightarrow (1 - x) \vec{A B} + x \vec{A C}$ $= \frac{k}{9} \vec{A B} + \frac{k}{4} \vec{A C}$ $\Leftrightarrow k = \frac{36}{13}$ , $x = \frac{9}{13} .$

Vậy $x = \frac{9}{13}$ là giá trị cần tìm.

Bài 2: Cho $Δ A B C$ lấy các điểm $I$ , $J$ thoả mãn $\vec{I A} = 2 \vec{I B}$ , $3 \vec{J A} + 2 \vec{J C} = \vec{0} .$ Chứng minh rằng $I J$ đi qua trọng tâm $G$ của $Δ A B C .$

Giải:

$\vec{I A} = 2 \vec{I B}$ $\Leftrightarrow \vec{I A} - 2 \vec{I B} = \vec{0} .$

$3 \vec{J A} + 2 \vec{J C} = \vec{0}$ $\Leftrightarrow 3 \vec{I A} + 2 \vec{I C} = 5 \vec{I J} .$

Suy ra $2 (\vec{I A} + \vec{I B} + \vec{I C}) = 5 \vec{I J}$ $\Leftrightarrow 6 \vec{I G} = 5 \vec{I J}$ $\Leftrightarrow I$ , $J$ , $G$ thẳng hàng.

Bài 3: Cho tam giác $A B C .$ Hai điểm $M$ , $N$ di động thỏa mãn:

$\vec{M N} = \vec{M A} + \vec{M B} + \vec{M C} .$

a) Chứng minh rằng $M N$ đi qua điểm cố định.

b) $P$ là trung điểm của $A M .$ Chứng minh rằng $M P$ đi qua điểm cố định.

Giải:

a) Gọi $G$ là trọng tâm tam giác $A B C$ suy ra:

$\vec{M N} = \vec{M A} + \vec{M B} + \vec{M C}$ $\Leftrightarrow \vec{M N} = \vec{G A} + \vec{G B} + \vec{G C} + 3 \vec{M G}$ $= 3 \vec{M G} .$

Suy ra $M$ , $N$ , $G$ thẳng hàng hay $M N$ đi qua điểm cố định $G .$

b) $P$ là trung điểm $A M$ $\Rightarrow \vec{M P} = \frac{1}{2} (\vec{M A} + \vec{M N})$ $= \frac{1}{2} (2 \vec{M A} + \vec{M B} + \vec{M C}) .$

Gọi $I$ là trung điểm $B C$ , $J$ là trung điểm $A I$ suy ra $2 \vec{J A} + \vec{J B} + \vec{J C} = \vec{0} .$

Do đó $\vec{M P} = 2 \vec{M J}$ suy ra $M P$ đi qua điểm cố định $J .$

Bài 4: Cho hai điểm $M$ , $P$ là hai điểm di động thỏa mãn:
$\vec{M P} = a \vec{M A} + b \vec{M B} + c \vec{M C} .$

Chứng minh rằng $M P$ đi qua điểm cố định.

Gọi $I$ là tâm đường tròn nội tiếp tam giác $A B C$ suy ra $a \vec{I A} + b \vec{I B} + c \vec{I C} = \vec{0} .$

Do đó $\vec{M P} = a \vec{M A} + b \vec{M B} + c \vec{M C}$ $\Leftrightarrow \vec{M P} = (a + b + c) \vec{M I} .$
Vậy $M P$ đi qua điểm cố định $I .$

Bài 5: Cho hình bình hành $A B C D .$ Gọi $E$ là điểm đối xứng của $D$ qua điểm $A$ , $F$ là điểm đối xứng của tâm $O$ của hình bình hành qua điểm $C$ và $K$ là trung điểm của đoạn $O B .$ Chứng minh ba điểm $E$ , $K$ , $F$ thẳng hàng và $K$ là trung điểm của $E F .$

Giải:

Ta có: $\vec{E F} = \frac{5}{2} \vec{A D} + \frac{3}{2} \vec{A B}$ , $\vec{E K} = \frac{5}{4} \vec{A D} + \frac{3}{4} \vec{A B} .$

$\Rightarrow \vec{E F} = 2 \vec{E K} .$

Vì vậy $K$ là trung điểm $E F .$

Bài 6: Cho hai tam giác $A B C$ và $A_{1} B_{1} C_{1}$ , $A_{2}$ , $B_{2}$ , $C_{2}$ lần lượt là trọng tâm các tam giác $B C A_{1}$ , $C A B_{1}$ , $A B C_{1} .$ Gọi $G$ , $G_{1}$ , $G_{2}$ lần lượt là trọng tâm các tam giác $A B C$ , $A_{1} B_{1} C_{1}$ , $A_{2} B_{2} C_{2} .$ Chứng minh rằng $G$ , $G_{1}$ , $G_{2}$ thẳng hàng và tính $\frac{G G_{1}}{G G_{2}} .$

Giải:

Vì $G$ , $G_{1}$ là trọng tâm tam giác $A B C$ , $A_{1} B_{1} C_{1}$ suy ra:

$3 \vec{G G_{1}} = \vec{G A_{1}} + \vec{G B_{1}} + \vec{G C_{1}} .$

$\Leftrightarrow 3 \vec{G G_{1}} = \vec{G A} + \vec{G B} + \vec{G C}$ $+ \vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}} .$

$\Leftrightarrow 3 \vec{G G_{1}} = \vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}} .$

Tương tự $G$ , $G_{2}$ là trọng tâm tam giác $A B C$ , $A_{2} B_{2} C_{2}$ suy ra:

$3 \vec{G G_{1}} = \vec{G A_{1}} + \vec{G B_{1}} + \vec{G C_{1}}$

$\Leftrightarrow 3 \vec{G G_{2}} = \vec{A A_{2}} + \vec{B B_{2}} + \vec{C C_{2}} .$

Mặt khác $\vec{A A_{2}} + \vec{B B_{2}} + \vec{C C_{2}}$ $= \vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}}$ $+ \vec{A_{1} A_{2}} + \vec{B_{1} B_{2}} + \vec{C_{1} C_{2}} .$

Mà $A_{2}$ , $B_{2}$ , $C_{2}$ lần lượt là trọng tâm các tam giác $B C A_{1}$ , $C A B_{1}$ , $A B C_{1} .$

Suy ra $3 (\vec{A_{1} A_{2}} + \vec{B_{1} B_{2}} + \vec{C_{1} C_{2}})$ $= 3 (\vec{A_{1} B} + \vec{A_{1} C} + \vec{B_{1} C} + \vec{B_{1} A} + \vec{C_{1} A} + \vec{C_{1} B}) .$

$= 6 (\vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}}) .$

Do đó $\vec{A A_{2}} + \vec{B B_{2}} + \vec{C C_{2}}$ $= 3 (\vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}})$ $\Rightarrow \vec{G G_{2}} = \vec{A A_{1}} + \vec{B B_{1}} + \vec{C C_{1}} .$

Vậy $\vec{G G_{2}} = 3 \vec{G G_{1}} .$

Bài 7: Cho tam giác $A B C .$ Các điểm $M$ , $N$ , $P$ lần lượt nằm trên đường thẳng $B C$ , $C A$ , $A B$ sao cho $\vec{M B} = α \vec{M C}$ , $\vec{N C} = β \vec{N A}$ , $\vec{P A} = γ \vec{P B} .$ Tìm điều kiện của $α$ , $β$ , $γ$ để $M$ , $N$ , $P$ thẳng hàng.

Giải:

Ta có: $\vec{M B} = \frac{α}{1 - α} \vec{B C}$ , $\vec{B P} = \frac{1}{γ - 1} \vec{A B}$ , $\vec{B C} = (1 - α) \vec{M C}$ , $\vec{C N} = \frac{β}{1 - β} \vec{A C} .$

Ta có:

$\vec{M N} = - \frac{1}{1 - α} \vec{A B} + (\frac{1}{1 - α} + \frac{β}{1 - β}) \vec{A C} .$

$\vec{M P} = (- \frac{α}{1 - α} - \frac{1}{1 - γ}) \vec{A B} + \frac{α}{1 - α} \vec{A C} .$

Để $M$ , $N$ , $P$ thẳng hàng thì ta phải có:
$\frac{- \frac{α}{1 - α} - \frac{1}{1 - γ}}{- \frac{1}{1 - α}}$ $= \frac{\frac{α}{1 - α}}{\frac{1}{1 - α} + \frac{β}{1 - β}}$ $\Leftrightarrow α β γ = 1.$

Bài 8: Cho tứ giác $A B C D$ ngoại tiếp đường tròn tâm $O .$ Chứng minh rằng trung điểm hai đường chéo $A C$ , $B D$ và tâm $O$ thẳng hàng.

Giải:

Gọi $P$ , $Q$ , $R$ , $S$ lần lượt là các tiếp điểm của các đoạn thẳng $A B$ , $B C$ , $C D$ , $D A$ đối với đường tròn tâm $O .$

Đặt $S A = A P = a$ , $B P = B Q = b$ , $C Q = C R = c$ , $D R = D S = d .$

Áp dụng định lý con nhím cho tứ giác $A B C D$ ta có:

$(a + b) \vec{O P} + (b + c) \vec{O Q}$ $ + (c + d)\overrightarrow {OR} + (d +

a)\overrightarrow {OS} = \vec 0.$

$\Leftrightarrow (a + b) (\frac{b}{a + b} \vec{O A} + \frac{a}{a + b} \vec{O B})$ $+ (b + c) (\frac{c}{b + c} \vec{O B} + \frac{b}{b + c} \vec{O C})$ $+ (c + d) (\frac{d}{c + d} \vec{O C} + \frac{c}{c + d} \vec{O D})$ $+ (d + a) (\frac{a}{d + a} \vec{O D} + \frac{d}{d + a} \vec{O A}) .$

$\Leftrightarrow (b + d) (\vec{O A} + \vec{O C})$ $+ (a + c) (\vec{O B} + \vec{O D}) = \vec{0} .$

$\Leftrightarrow (b + d) \vec{O M} + (a + c) \vec{O N} = \vec{0} .$

Suy ra $O$ , $M$ , $N$ thẳng hàng.

Bài 9: Cho lục giác $A B C D E F$ nội tiếp đường tròn tâm $O$ thỏa mãn $A B = C D = E F .$ Về phía ngoài lục giác dựng các tam giác $A M B$ , $B N C$ , $C P D$ , $D Q E$ , $E R F$ , $F S A$ đồng dạng và cân tại $M$ , $N$ , $P$ , $Q$ , $R$ , $S .$ Gọi $O_{1}$ , $O_{2}$ lần lượt là trọng tâm tam giác $M P R$ và $N Q S .$ Chứng minh rằng ba điểm $O$ , $O_{1}$ , $O_{2}$ thẳng hàng.

Giải:

Gọi $M_{1}$ , $N_{1}$ , $P_{1}$ , $Q_{1}$ , $R_{1}$ , $S_{1}$ lần lượt là hình chiếu của $M$ , $N$ , $P$ , $Q$ , $R$ , $S$ lên $A B$ , $B C$ , $C D$ , $D E$ , $E F$ , $F A .$ Suy ra $M_{1}$ , $N_{1}$ , $P_{1}$ , $Q_{1}$ , $R_{1}$ , $S_{1}$ lần lượt là trung điểm của $A B$ , $B C$ , $C D$ , $D E$ , $E F$ , $F A .$

Ta có: $\vec{M S} + \vec{R Q} + \vec{P N}$ $= (\vec{M M_{1}} + \vec{M_{1} A} + \vec{A S_{1}} + \vec{S_{1} S})$ $+ (\vec{R R_{1}} + \vec{R_{1} E} + \vec{E Q_{1}} + \vec{Q_{1} Q})$ $+ (\vec{P P_{1}} + \vec{P_{1} C} + \vec{C N_{1}} + \vec{N_{1} N})$ (vì theo định lí con nhím thì $\vec{M M_{1}} + \vec{P P_{1}} + \vec{R R_{1}} + \vec{N_{1} N} + \vec{Q_{1} Q} + \vec{S_{1} S} = \vec{0}$ ).

Mặt khác $A B = C D = E F$ suy ra $\frac{M M_{1}}{O M_{1}} = \frac{R R_{1}}{O R_{1}} = \frac{P P_{1}}{O P_{1}} = \frac{1}{k} .$

Do đó $\vec{M S} + \vec{R Q} + \vec{P N}$ $= k (\vec{O M} + \vec{O P} + \vec{O R}) .$

$\Leftrightarrow \vec{O S} + \vec{O Q} + \vec{O N}$ $= (k + 1) (\vec{O M} + \vec{O P} + \vec{O R})$ $\Leftrightarrow \vec{O O_{2}} = (k + 1) \vec{O O_{1}} .$

Hay ba điểm $O$ , $O_{1}$ , $O_{2}$ thẳng hàng.

Toán lớp 10 - Tags: thẳng hàng, vectơ

Ứng dụng vectơ để chứng minh 3 điểm thẳng hàng, đi qua điểm cố định – Toán lớp 10

1. PHƯƠNG PHÁP GIẢI

2. Ví dụ chứng minh 3 điểm thẳng hàng

3. BÀI TẬP LUYỆN TẬP

Ứng dụng vectơ để chứng minh hai đường thẳng song song, 3 đường thẳng đồng quy – Toán lớp 10

Cách chứng minh đẳng thức véctơ – Toán lớp 10

Đề cương ôn tập HK2 môn Toán lớp 10

244 câu trắc nghiệm Đại số lớp 10 chương 3 có lời giải

Chuyên đề Hàm số lượng giác – Toán lớp 10

Phương pháp giải toán hình học trên tọa độ Oxy lớp 10

Bài tập trắc nghiệm Số gần đúng và Sai số – Đại số 10