Ôn tập: Tứ giác nội tiếp
1. Tứ giác nội tiếp là tứ giác có 4 đỉnh nằm trên một đường tròn.
2. Tứ giác ABCD nội tiếp đồng nghĩa 4 điểm A; B; C và D cùng nằm trên 1 đường tròn.
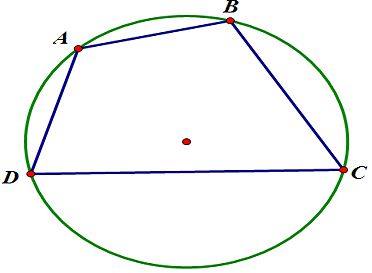
3. Tứ giác nội tiếp đường tròn thì đường tròn gọi là ngoại tiếp tứ giác đó.
4. Tâm của đường tròn ngoại tiếp tứ giác là giao điểm ba đường trung trực của ba cạnh tứ giác đó.
5. Cho tứ giác ABCD nội tiếp (O; R) khi đó OA= OB= OC = OD =R.
6. Chú ý: O có thể nằm ngoài tứ giác; cũng có thể nằm trong hoặc nằm trên một cạnh chứ không phải lúc nào cũng nằm trong.
7. Cho ABCD là tứ giác nội tiếp thì A+C= B+D = 1800.
8. Ngược lại tứ giác ABCD có A+C =1800 hoặc B+D=1800 thì ABCD nội tiếp.
9. Để c/m tứ giác ABCD nội tiếp ta có các cách sau:
a. Chỉ ra A+C =1800.
b. Chỉ ra B+D=1800.
c. Chỉ ra bốn điểm A; B;C và D cùng thuộc một đường tròn nào đó cụ thể.
d. Chỉ ra các góc nội tiếp tại A và B cùng nhìn CD 1 góc bằng nhau.
Bài tập:
1. Cho ΔABC có AB>AC. Vẽ ba đường cao AH; BK và CF; I là trực tâm ΔABC. Nêu tên các tứ giác nội tiếp đường tròn khi nối HK; KF và FH.
2. cho góc nhọn xOy. Trên cạnh Ox lấy A và B: OA=2cm; OB=6cm. trên Oy lấy hai điểm C và D: OC=3cm; OD=4cm. nối BD và AC. c/m: ABCD nội tiếp.
3. Cho (O) và A ∈ (O). Từ M trên tiếp tuyến tại A vẽ cát tuyên MBC. Gọi I là trung điểm BC. C/m: AMIO nội tiếp.