Một số hệ thức về cạnh và đường cao trong tam giác vuông

Xét tam giác ABC vuông tại A, cạnh huyền BC = a, các cạnh góc vuông AC = b và AB = c. Gọi AH = h là đường cao ứng với cạnh huyền và CH = b’, BH = c’ lần lượt là hình chiếu của AC, AB trên cạnh huyền BC.

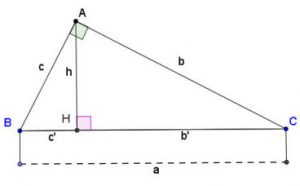
Trong tam giác vuông, nếu biết hai cạnh, hoặc một cạnh và một góc nhọn thì có thể tính được các góc và các cạnh còn lại của tam giác đó. Bằng các định lí dưới đây:

1. Định lí về hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền

Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền: $ \displaystyle b_{{}}^{2}$ = ab’; $ \displaystyle c_{{}}^{2}$ = ac’

2. Một số hệ thức liên quan tới đường cao

Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền: $ \displaystyle h_{{}}^{2}$ = b’.c’
Trong tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng: bc = ah
Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông: $ \displaystyle \frac{1}{h_{{}}^{2}}=\frac{1}{b_{{}}^{2}}+\frac{1}{c_{{}}^{2}}$