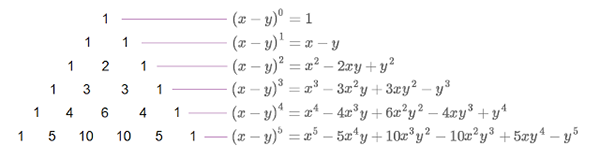Lý thuyết nhị thức Newton và tam giác Pascal
Tóm tắt kiến thức về nhị thức Newton
I. Nhị thức Newton
1. Công thức nhị thức Newton
Với a, b là những số thực tùy ý và với mọi số tự nhiên n ≥ 1, ta có:
$(a + b)^n$ = $C_{n}^{0}a^n+C_{n}^{1}a^{n-1}b+C_{n}^{2}a^{n-2}b{^2}+…+C_{n}^{n-1}ab^{n-1}+C_{n}^{n}b{^n} $ (1)
2. Quy ước
Với a là số thực khác 0 và n là số tự nhiên khác 0, ta quy ước:
$a^0$ = 1; $ \displaystyle {{a}^{-n}}=\frac{1}{{{a}^{n}}}$
3. Chú ý
Với các điều kiện và quy ước ở trên, đồng thời thêm điều kiện a và b đều khác 0, có thể viết công thức (1) ở dạng sau đây:
${(a + b)}^n$ = $\displaystyle\sum\limits_{k=0}^{n}C_{n}^{k}a^{n-k}b^{k}$ = $\displaystyle\sum\limits_{k=0}^{n}C_{n}^{k}a^{k}b^{n-k}$
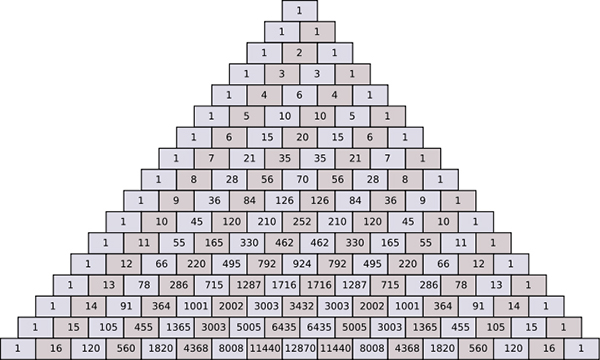
II. Tam giác Pascal
1. Mô hình của tam giác Pascal
Ứng dụng tam giác pascal khai triển ${(x-y)}^n$
2. Cấu tạo của tam giác Pascal
– Số đầu tiên và cuối cùng đều bằng 1
– Xét hai số ở cột k và cột k + 1, đồng thời cùng thuộc dòng n, (k ≥ 0; n ≥1), ta có: tổng của hai số này bằng số đứng ở giao của cột k + 1 và dòng n + 1.
3. Tính chất của tam giác Pascal
Từ cấu tạo của tam giác Pascal, có thể chứng minh được rằng:
a) Giao của dòng n và cột k là $C_{n}^{k}$
b) Các số của tam giác Pascal thỏa mãn công thức Pascal:
$C_{n}^{k}$ + $C_{n}^{k+1}$ = $C_{n+1}^{k+1}$
c) Các số ở dòng n là các hệ số trong khai triển của nhị thức $(a + b)^{n}$ (theo công thức nhị thức Newton), với a, b là hai số thực tùy ý. Chẳng hạn, các số ở dòng 4 là các hệ số trong khai triển của $(a + b)^{4}$ (theo công thức nhị thức Niu – Tơn) dưới đây:
$(a + b)^{4}$ = $a^{4} + 4a^{3}b + 6a^{2}b^{2} + 4ab^{3} + b^{4}$