Đề thi Toán vào lớp 10 tại Hà Nội từ năm 1988 đến nay

Đề thi Toán vào 10 Hà Nội năm học 1990-1991

Bài 1:
Xét biểu thức:
P = ($ \frac{\sqrt{x}-1}{3\sqrt{x}-1}-\frac{1}{3\sqrt{x}+1}+\frac{5\sqrt{x}}{9x-1}$) : (1-$ \frac{3\sqrt{x}-2}{3\sqrt{x}+1}$)
a/ Rút gọn P.
b/ Tìm các giá trị của x để P = $ \frac{6}{5}$
Bài 2:
Một xe tải và một xe con cùng khởi hành từ tỉnh A đến tỉnh B. Xe đi với vận tốc 30km/h, xe con đi với vận tốc 45km/h. Sau khi đi được ¾ quãng đường AB, xe con tăng vận tốc thêm 5km/h trên quãng đường còn lại. Tính quãng đường AB, biết rằng xe con đến tỉnh B sớm hơn xe tải 2 giờ 20 phút.
Bài 3:
Cho đường tròn (O), một dây AB và một điểm C ở ngoài tròn nằm trên tia AB. Từ điểm chính giữa của  cung lớn AB kẻ đường kính PQ của đường tròn , cắt dây AB tại D.Tia CP cắt đường tròn tại điểm thứ hai I.Các dây AB và QI cắt nhau tại K.
a/ Cm tứ giác PDKI nội tiếp được.
b/ Cm CI.CP = CK.CD
c/ Cm  IC là tia phân giác của góc ở ngoài đỉnh I của tam giác AIB
d/ Giả sử A,B,C cố định. Cmr khi đường tròn (O)thay đổi nhưng vẫn đi qua B thì đường thẳng QI luôn đi qua một điểm cố định.
Bài 4:
Tìm giá trị của x để biểu thức
y = x – $ \sqrt{x-1991}$ đạt giá trị nhỏ nhất và tìm GTNN đó.
Gợi ý giải:
Bài 1:
1/ Đk: x ≠ 1/9  =>   P = ($ \frac{\sqrt{x}-1}{3\sqrt{x}-1}-\frac{1}{3\sqrt{x}+1}+\frac{5\sqrt{x}}{9x-1}$) : (1- $ \frac{3\sqrt{x}-2}{3\sqrt{x}+1}$)
=  $ \frac{(\sqrt{x}-1)(3\sqrt{x}+1)-(3\sqrt{x}-1)+5\sqrt{x}}{(3\sqrt{x}-1)(3\sqrt{x}+1)}$  :  $ \frac{3\sqrt{x}+1-3\sqrt{x}+2}{3\sqrt{x}+1}$
=  $ \frac{3x+\sqrt{x}-3\sqrt{x}-1-3\sqrt{x}+1+5\sqrt{x}}{(3\sqrt{x}-1)(3\sqrt{x}+1)}$ . $ \frac{3\sqrt{x}+1}{3}$ = $ \frac{3x}{(3\sqrt{x}-1)(3\sqrt{x}+1)}$ . $ \frac{3\sqrt{x}+1}{3}$  = $ \frac{x}{3\sqrt{x}-1}$
2/ P = $ \frac{6}{5}$ ⇔ $ \frac{x}{3\sqrt{x}-1}$ = $ \frac{6}{5}$ => 5x – 6 ($ 3\sqrt{x}-1$) = 0 ⇔ 5x – 18$ \sqrt{x}$ +6 = 0
Δ =     ⇒ $ \sqrt{x}$  =
Bài 2:
Gọi quãng đường AB là x(km, x > 0)
Ta có phương trình: $ \frac{x}{30}=\frac{3}{4}.\frac{x}{45}+\frac{1}{4}.\frac{x}{50}+2\frac{1}{3}$
Bài 3:

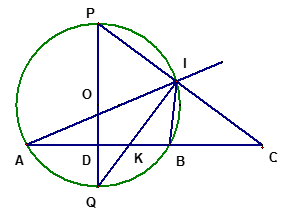
Hình vẽ bài 3

a/ tứ giác PDKI nội tiếp được vì $ \displaystyle \widehat{PDK}=\widehat{PIK}$ = 90°
b/ CI.CP = CK.CD vì  ΔICK ~  ΔDCP
c/ IC là tia pg vì IQ là pg $ \displaystyle \widehat{AIB}$ và IC ⊥ IQ
d/  K là điểm cố định vì IC, IK là các phân giác trong và ngoài tại I của tam giác AIB ( chia điều hòa) $ \frac{KB}{KA}=\frac{IB}{IA}=\frac{CB}{CA}$ mà A,B,C cố định.
Bài 4:
Tìm giá trị của x để biểu thức
y = x – $ \sqrt{x-1991}$ đạt giá trị nhỏ nhất
y = x – $ \sqrt{x-1991}$  =  [( x – 1991)- $ \sqrt{x-1991}$ + $ \frac{1}{4}$] –  $ \frac{1}{4}$ + 1991
= ($ \sqrt{x-1991}$ – $ \frac{1}{2}$)² + $ 1990\frac{3}{4}$ ≥ $ \frac{1}{4}$ + $ 1990\frac{3}{4}$ = 1991
⇒ Min y = 1991 khi x = 1991