Đề thi Toán vào lớp 10 tại Hà Nội từ năm 1988 đến nay

Đề thi Toán vào 10 Hà Nội năm học 1989-1990

Bài 1:
Cho biểu thức
A = 1- ($ \frac{2}{1+2x}-\frac{5x}{4{{x}^{2}}-1}-\frac{1}{1-2x}$) : $ \frac{x-1}{4{{x}^{2}}+4x+1}$
a/ Rút gọn A và nêu các điều kiện phải có của x.
b/ Tìm giá trị của x để A = $ -\frac{1}{2}$
Bài 2:
Một ô tô dự định đi từ tỉnh A đến tỉnh B với vận tốc 50km/h. Sau khi đi được 2/3 quãng đường với vận tốc đó, vì đường khó đi nên người lái xe phải giảm vận tốc mỗi giờ 10km trên quãng đường còn lại. Do đó ô tô đến tỉnh B chậm hơn 30 phút so với dự định. Tính quãng đường AB.
Bài 3:
Cho hình vuông ABCD và một điểm E bất kỳ trên cạnh BC. Tia Ax vuông góc với AE cắt cạnh CD kéo dài tại F. Kẻ trung tuyến AI của  tam giác AEF và kéo dài cắt cạnh CD tại K.Đường thẳng qua E và song song với AB cắt AI tại G.
a/ Chứng minh AE = AF.
b/Chứng minh tứ giác EGFK là hình thoi.
c/ Chứng minh tam giác AKF và CAF đồng dạng và AF2 = KF.CF
d/Giả sử E chuyển động trên cạnh BC, chứng minh rằng FK = BE + DK và chu vi tam giác ECK không đổi.
Bài 4:
Tìm giá trị của x để biểu thức y= $ \frac{{{x}^{2}}-2x+1989}{{{x}^{2}}}$  (Đk x ≠ 0) đạt giá trị nhỏ nhất và tìm GTNN đó.
Gợi ý giải:
Bài 1:
A = 1- ($ \frac{2}{1+2x}-\frac{5x}{4{{x}^{2}}-1}-\frac{1}{1-2x}$) : $ \frac{x-1}{4{{x}^{2}}+4x+1}$
1/Đk  x ≠ $ \displaystyle \pm \frac{1}{2}$ và x ≠ 1
A = 1- ($ \frac{2}{1+2x}-\frac{5x}{(2x-1)(2x+1)}+\frac{1}{2x-1}$) : $ \frac{x-1}{{{(2x+1)}^{2}}}$
=  1- $ \frac{2(2x-1)-5x+2x+1}{(2x-1)(2x+1)}$ . $ \frac{{{(2x+1)}^{2}}}{x-1}$ =  1- $ \frac{4x-2-5x+2x+1}{(2x-1)(2x+1)}$ . $ \frac{{{(2x+1)}^{2}}}{x-1}$
=  1- $ \frac{x-1}{(2x-1)(2x+1)}$ . $ \frac{{{(2x+1)}^{2}}}{x-1}$ =  1- $ \frac{2x+1}{2x-1}$ = $ \frac{-2}{2x-1}$
2/ A = -$ \frac{1}{2}$ ⇔ $ \frac{-2}{2x-1}$ = -$ \frac{1}{2}$ ⇔ 2x – 1 = 4 ⇔ x =  2,5
Bài 2:
Gọi quãng đường AB là x (km và x >0 )
Ta có phương trình:
$ \frac{2}{3}x:50+\frac{1}{3}x:40=\frac{x}{50}+\frac{1}{2}$ ⇔ $ \frac{2x}{150}+\frac{x}{120}=\frac{x}{50}+\frac{1}{2}$
Bài 3:

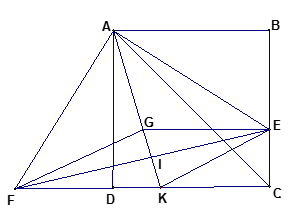
Đề thi Toán vào lớp 10 tại Hà Nội từ năm 1988 đến nay-2

Hình vẽ bài 3

a/ AE = AF. Vì $ \displaystyle \widehat{FAD}=\widehat{EAB}$ (cùng phụ với $ \displaystyle \widehat{DAE}$)
=> ΔADB =  ΔABE (cạnh gv- gn ) => k luận.
b/ Các tam giác vuông IGE & IKF bằng nhau (GE // KT
IE = IF) => GF = GE =KF = KE (vì AK là trung trực).
c/ Tam giác AKF và CAF đồng dạng và AF2 = KF.CF
Vì ABCD là hình vuông =>  goc ACF = 45°
Vì tam giác AEF vuông cân & AI là trung trực

d/ FD = BE (Vì 2 tam giác bằng nhau) => FK = BE+DK

Bài 4: y =  $ \frac{{{x}^{2}}-2x+1989}{{{x}^{2}}}$ (Đk x ≠ 0 => y ≠ 0 ) đạt giá trị nhỏ nhất ⇔ $ \frac{1}{y}$ đạt giá trị lớn nhất
⇔ $ \frac{{{x}^{2}}}{{{x}^{2}}-2x+1989}$ max ⇔ $ \frac{1}{1-\frac{2}{x}+\frac{1989}{{{x}^{2}}}}$ max ⇔ $ 1-\frac{2}{x}+\frac{1989}{{{x}^{2}}}$ min
Mà $ 1-\frac{2}{x}+\frac{1989}{{{x}^{2}}}$ = $ \frac{1989}{{{x}^{2}}}-\frac{2}{x}+\frac{1989.(1988+1)}{{{1989}^{2}}}$  = 1989 ($ \frac{1}{{{x}^{2}}}-2.\frac{1}{x}.\frac{1}{1989}+\frac{1}{{{1989}^{2}}}$) + $ \frac{1988}{1989}$
= 1989. ($ \frac{1}{{{x}^{{}}}}-\frac{1}{{{1989}^{{}}}}$)2 + $ \frac{1988}{1989}$ ≥ $ \frac{1988}{1989}$ => Min y = $ \frac{1989}{1988}$  khi x = 1989.

Đề thi Toán vào lớp 10 - Tags: