Đề thi Toán vào lớp 10 tại Hà Nội từ năm 1988 đến nay

Tổng hợp toàn bộ đề thi Toán vào lớp 10 tại thành phố Hà Nội từ năm 1988 đến nay. Có kèm theo gợi ý giải, đáp án.

Mỗi trang là một đề thi theo thứ tự bắt đầu từ đề thi năm 1988, cùng với đề thi là đáp án ngay bên dưới. Timgiasuhanoi.com sẽ cập nhật thêm đề thi các năm tiếp theo.

Đề thi Toán vào 10 Hà Nội năm học 1988-1989

Bài 1:
Cho  A = $ \left( \frac{2+x}{2-x}-\frac{2-x}{2+x}-\frac{4{{x}^{2}}}{{{x}^{2}}-4} \right):\frac{x-3}{2x-{{x}^{2}}}$
a/ Rút gọn A.
b/ Tính giá trị của A khi |x| = 1
Bài 2:
Một chiếc xe tải đi từ tỉnh A đến B với vận tốc 40km/h.. Sau đó 1giờ 30 phút, một chiếc xe con cũng khởi hành từ tỉnh A  để đi đến tỉnh B với vận tốc 60km/h. Hai xe gặp nhau khi chúng đã đi được một nửa quãng đường AB.
Tính quãng đường AB.
Bài 3:
Cho tứ giác ABCD nội tiếp trong một đường tròn và P là trung điểm của cung AB không chứa C và D. Hai dây PC và PD lần lượt cắt AB tại E và F. Các dây AD và PC kéo dài cắt nhau tại I: các dây BC và PD kéo dài cắt nhau tại K. Chứng minh rằng:
a/ Góc CID bằng góc CKD.
b/ Tứ giác CDFE nội tiếp được.
c/ IK // AB.
d/ Đường tròn ngoại tiếp tam giác AFD tiếp xúc với PA tại A.
Bài 4:
Tìm giá trị của x để biểu thức :
M = ( 2x – 1)² – 3 |2x-1| + 2
Đạt giá trị nhỏ nhất và tìm GTNN đó.
Gợi ý giải:
Bài 1:
1/  Đk: x ≠ 0 ; x ≠ ±2 và x ≠ 3
A = $ \left( \frac{2+x}{2-x}-\frac{2-x}{2+x}-\frac{4{{x}^{2}}}{{{x}^{2}}-4} \right):\frac{x-3}{2x-{{x}^{2}}}$ = $ \left( \frac{2+x}{2-x}-\frac{2-x}{2+x}+\frac{4{{x}^{2}}}{(2-x)(2+x)} \right):\frac{x-3}{x(2-x)}$
= $ \displaystyle \frac{{{(2+x)}^{2}}-{{(2-x)}^{2}}+4{{x}^{2}}}{(2-x)(2+x)}.\frac{x(2-x)}{x-3}$ = $ \displaystyle \frac{{{x}^{2}}+4x+4-{{x}^{2}}+4x-4+4{{x}^{2}}}{(2-x)(2+x)}.\frac{x(2-x)}{x-3}$
= $ \displaystyle \frac{4{{x}^{2}}+8x}{(2-x)(2+x)}.\frac{x(2-x)}{x-3}$ = $ \displaystyle \frac{4x(x+2)}{(2-x)(2+x)}.\frac{x(2-x)}{x-3}$ = $ \displaystyle \frac{4{{x}^{2}}}{x-3}$
2/ |x| = 1=> $ \displaystyle \left\{ \begin{array}{l}A=\frac{4}{1-3}=-2\\A=\frac{4}{-1-3}=-1\end{array} \right.$
Bài 2:
Gọi độ dài quãng đường AB là x (km ; x > 0)
Ta có phương trình: $ \frac{x}{2}:40-\frac{x}{2}:60=\frac{3}{2}$
Bài 3:

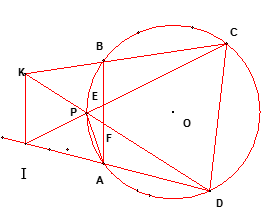
Hình vẽ bài 3

a/ $ \widehat{CID}=\widehat{CKD}$ vì là các góc chắn các cung bằng nhau.(=> CDIK nội tiếp)
b/  Tứ giác CDEF nội tiếp được vì góc ngoài bằng góc trong không kề với nó.
c/ IK//AB vì tứ giác CDIK nội tiếp => $ \displaystyle \widehat{IKD}=\widehat{ICD}$ và $ \displaystyle \widehat{ICD}=\widehat{PFB}$ ( tứ giác CDEF nội tiếp)  => K luận .
d/ AF là tt đt(AFD) vì $ \displaystyle \widehat{EAF}=\widehat{ADF}$ (nt chắn các cung bằng nhau).
Bài 4:
M = ( 2x – 1)² – 3 |2x-1| + 2 = (| 2x – 1|)² – 3 |2x-1| $ \displaystyle \frac{9}{4}-\frac{1}{4}$
= (|2x – 1| – $ \displaystyle \frac{3}{2}$)²  – $ \displaystyle \frac{1}{4}$ ≥ $ \displaystyle -\frac{1}{4}$
Dấu “ = ” xảy ra khi  (|2x – 1| – $ \displaystyle \frac{3}{2}$)²  = 0 ⇔ | 2x – 1| = $ \displaystyle \frac{3}{2}$
⇔ 2x – 1 = $ \displaystyle \pm \frac{3}{2}$ ⇔ $ \displaystyle \left[ \begin{array}{l}2x-1=\frac{3}{2}\\2x-1=-\frac{3}{2}\end{array} \right.$
⇔ $ \displaystyle \left[ \begin{array}{l}{{x}_{1}}=\frac{5}{4}\\{{x}_{2}}=-\frac{1}{4}\end{array} \right.$