Đề thi Toán vào lớp 10 Đà Nẵng năm học 2014-2015
Đề thi tuyển sinh vào lớp 10 môn Toán TP. Đà Nẵng năm học 2014-2015
Thời gian làm bài: 120 phút (không kể thời gian giao đề)
Bài 1: (1,5 điểm)
1) Tính giá trị của biểu thức
2) Rút gọn biểu thức
Bài 2: (1,0 điểm)
Giải hệ phương trình:
Bài 3: (2,0 điểm)
Cho hàm số y = x2 có đồ thị (P) và hàm số y = 4x + m có đồ thị (dm)
1) Vẽ đồ thị (P)
2)Tìm tất cả các giá trị của m sao cho (dm) và (P) cắt nhau tại hai điểm phân biệt, trong đó tung độ của một trong hai giao điểm đó bằng 1.
Bài 4: (2,0 điểm)
Cho phương trình x2 + 2(m – 2)x – m2 = 0, với m là tham số.
1) Giải phương trình khi m = 0.
2)Trong trường hợp phương trình có hai nghiệm phân biệt x1 và x2 với x1 < x2, tìm tất cả các giá trị của m sao |x1| – |x2| = 6
Bài 5: (3,5 điểm)
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC). Vẽ đường tròn (C) có tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai là D.
1) Chứng minh BD là tiếp tuyến của đường tròn (C).
2) Trên cung nhỏ
a) BA2 = BE.BF và
b) Ba đường thẳng AF, ED và HK song song với nhau từng đôi một.
Gợi ý giải:
Bài 1:
1) A = 3 – 2 = 1
2) Với điều kiện đã cho thì
Bài 2:
Bài 3:
1)
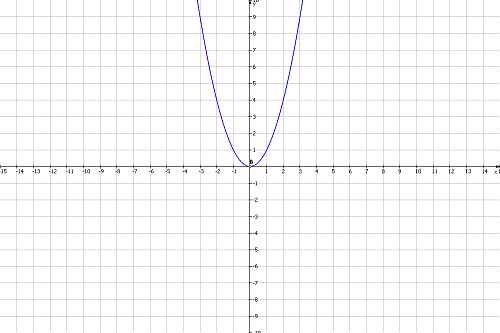
2) Phương trình hoành độ giao điểm của y = x2 và đường thẳng y = 4x + m là :
x2 = 4x + m ⇔ x2 – 4x – m = 0 (1)
(1) có
Để (dm) và (P) cắt nhau tại hai điểm phân biệt thì
y = 4x + m = 1 => x =
Yêu cầu của bài toán tương đương với
⇔
Bài 4:
1) Khi m = 0, phương trình thành : x2 – 4x = 0 x = 0 hay x – 4 = 0 x = 0 hay x = 4
2)
Vậy phương trình luôn có hai nghiệm phân biệt với mọi m.
Ta có
Ta có
Khi m = -1 ta có
Khi m = 5 ta có
Vậy m = 5 thỏa yêu cầu bài toán.
Bài 5:
1) Ta có
BC vuông góc với AD nên H là trung điểm AD. Suy ra
2)
a)
Trong tam giác vuông ABC ta có
Xét hai tam giác đồng dạng ABE và FBA
vì có góc B chung
và
suy ra
Từ (1) và (2) ta có BH.BC = BE.FB
Từ BE.BF= BH.BC
2 tam giác BEH và BCF đồng dạng vì có góc B chung và
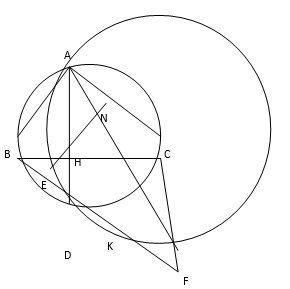
b) Do kết quả trên ta có
Gọi giao điểm của AF và EH là N. Ta có 2 tam giác ΔHED và ΔHNA bằng nhau
(vì góc H đối đỉnh, HD = HA,
Suy ra HE = HN, nên H là trung điểm của EN. Suy ra HK là đường trung bình của tam giác EAF.
Vậy HK // AF.
Vậy ED // HK // AF.