Đề thi học sinh giỏi Toán lớp 6 số 1 hay (có đáp án)

Thời gian làm bài 120 phút.

Câu 1: (2 điểm) Cho biểu thức ${\displaystyle A=\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}}$

a, Rút gọn biểu thức

b, Chứng minh rằng nếu a là số nguyên thì giá trị của biểu thức tìm được của câu a, là một phân số tối giản.

Câu 2: (1 điểm)

Tìm tất cả các số tự nhiên có 3 chữ số ${\displaystyle \overline{abc}}$ sao cho ${\displaystyle \overline{abc}=n^2-1}$ và ${\displaystyle \overline{cba}={(n-2)}^2}$

Câu 3: (2 điểm)

a. Tìm n để n² + 2006 là một số chính phương

b. Cho n là số nguyên tố lớn hơn 3. Hỏi n² + 2006 là số nguyên tố hay là hợp số.

Câu 4: (2 điểm)

a. Cho a, b, n ∈ N^* Hãy so sánh ${\displaystyle \frac{a+n}{b+n}}$ và ${\displaystyle \frac{a}{b}}$

b. Cho A = ${\displaystyle \frac{{10}^{11}-1}{{10}^{12}-1}}$; B = ${\displaystyle \frac{{10}^{10}+1}{{10}^{11}+1}}$. So sánh A và B.

Câu 5: (2 điểm)

Cho 10 số tự nhiên bất kỳ :     a₁, a₂, ….., a₁₀. Chứng minh rằng thế nào cũng có một số  hoặc tổng một số các số liên tiếp nhau trong dãy trên chia hết cho 10.

Câu 6: (1 điểm)

Cho 2006 đường thẳng trong đó bất kì 2 đường thẳng nào cũng cắt nhau. Không có 3 đường thẳng nào đồng qui. Tính số giao điểm của chúng.

Đáp án Đề thi học sinh giỏi Toán lớp 6 số 1:

Câu 1:

Ta có: ${\displaystyle A=\frac{a^3+2a^2-1}{a^3+2a^2+2a+1}}$ = ${\displaystyle \frac{(a+1)(a^2+a-1)}{(a+1)(a^2+a+1)}=\frac{a^2+a-1}{a^2+a+1}}$

Điều kiện đúng a ≠  -1   ( 0,25 điểm).

Rút gọn đúng cho  0,75 điểm.

b.Gọi d là ước chung lớn nhất của  a² + a – 1 và a²+a +1               (0,25đ).

Vì a² + a – 1 =  a(a+1) – 1   là số lẻ nên d là số lẻ

Mặt khác, 2 =  [ a²+a +1 – (a² + a – 1) ] ${\displaystyle ⋮}$ d

Nên d = 1 tức là a² + a + 1  và a² + a – 1   nguyên tố cùng nhau.     (0,5đ)

Vậy biểu thức A là phân số tối giản. ( 0,25 điểm)

Câu 2:

${\displaystyle \overline{abc}}$ =  100a + 10 b + c = n² – 1                      (1)

${\displaystyle \overline{cba}}$ =  100c + 10 b + c = n² – 4n + 4    (2)                          (0,25đ)

Từ (1) và (2) ⇒ 99(a – c) = 4 n – 5 ⇒ 4n – 5 ${\displaystyle ⋮}$ 99 (3)     (0,25đ)

Mặt khác:  100 ≤ n²-1 ≤ 999 ⇔ 101 ≤ n² ≤ 1000 ⇔ 11 ≤ n ≤ 31 ⇔ 39 ≤ 4n – 5 ≤ 119 (4)   ( 0,25đ)

Từ (3) và (4) ⇒ 4n – 5  =  99 ⇒ n = 26

Vậy: ${\displaystyle \overline{abc}}$ = 675   ( 0,25đ)

Câu 3: (2 điểm)

a) Giả sử n² + 2006 là số chính phương khi đó ta đặt n² + 2006 = a² ( a ∈ Z) ⇔ a² – n² = 2006 ⇔ (a-n) (a+n) = 2006 (*) (0,25 điểm).

+ Thấy : Nếu a, n khác tính chất chẵn lẻ thì vế trái của (*) là số lẻ nên không thỏa mãn (*)  ( 0,25 điểm).

+ Nếu a,n cùng tính chẵn hoặc lẻ thì (a-n)2 và (a+n) 2 nên vế trái chia hết cho 4 và vế phải không chia hết cho 4 nên không thỏa mãn (*)  (0,25 điểm).

Vậy không tồn tại n để n² + 2006 là số chính phương. (0,25 điểm).

b) n là số nguyên tố > 3 nên không chia hết cho 3. Vậy n² chia hết cho 3 dư 1 do đó n² + 2006 = 3m + 1 + 2006 = 3m+2007= 3( m+669) chia hết cho 3.

Vậy n² + 2006 là hợp số. ( 1 điểm).

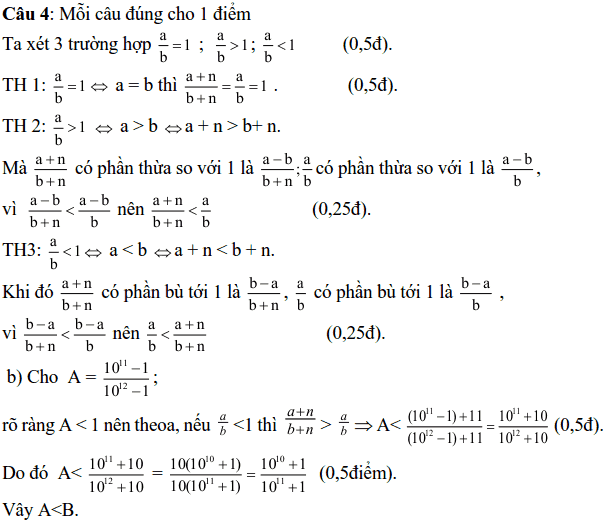
Câu 5: Lập dãy số .

Đặt

B₁ = a_1.

B₂ = a₁  + a₂ .

B₃ = a₁ + a₂ + a₃

……………………………..

B₁₀ = a₁ + a₂ + … + a₁₀ .

Nếu tồn tại B_i ( i= 1,2,3…10). nào đó chia hết cho 10 thì bài toán được chứng minh.   ( 0,25 điểm).

Nếu không tồn tại B_i nào chia hết cho 10 ta làm như sau:

Ta đen B_i chia cho 10 sẽ được 10 số dư ( các số dư ∈ { 1,2.3…9}). Theo nguyên tắc Diriclê, phải có ít nhất 2 số dư bằng nhau. Các số  B_m -B_n,  chia hết cho 10 ( m>n) ⇒ ĐPCM.

Câu 6: Mỗi đường thẳng cắt 2005 đường thẳng còn lại tạo nên 2005 giao điểm. Mà có 2006 đường thẳng ⇒ có : 2005x 2006 giao điểm. Nhưng mỗi giao điểm được tính 2 lần ⇒ số giao điểm thực tế là:

(2005x 2006):2 = 1003 x 2005 = 2011015 giao điểm.

• Đề kiểm tra chất lượng kì II môn Toán 6 THPT chuyên Amsterdam năm 2017-2018

• Đề thi HSG môn Toán 12 tỉnh Nam Định năm 2017-2018

• Bộ đề thi vào lớp 10 môn Toán tỉnh Thanh Hoá từ 2000 tới 2017

• Bộ đề ôn thi tuyển sinh vào lớp 10 THPT và THPT chuyên

• Đề thi HSG môn Toán 11 tỉnh Nghệ An năm 2017-2018

• 100 đề thi thử THPT quốc gia 2018 môn Toán – Trần Điệu Hoàng

• Đề thi giáo viên dạy giỏi trường mầm non Sơn Lâm năm 2017 – 2018