Đề cương ôn tập chương 1 Hình học 8 THCS Yên Nghĩa 2017-2018

Đề cương ôn tập chương 1 môn Hình học 8 trường THCS Yên Nghĩa, quận Hà Đông, TP Hà Nội, năm học 2017-2018.

I. Kiến thức cơ bản

– Định nghĩa, tính chất và dấu hiệu nhận biết các tứ giác đặc biệt.

– Định nghĩa, tính chất đường trung bình của tam giác, của hình thang.

– Tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông.

SƠ ĐỒ NHẬN BIẾT CÁC LOẠI TỨ GIÁC

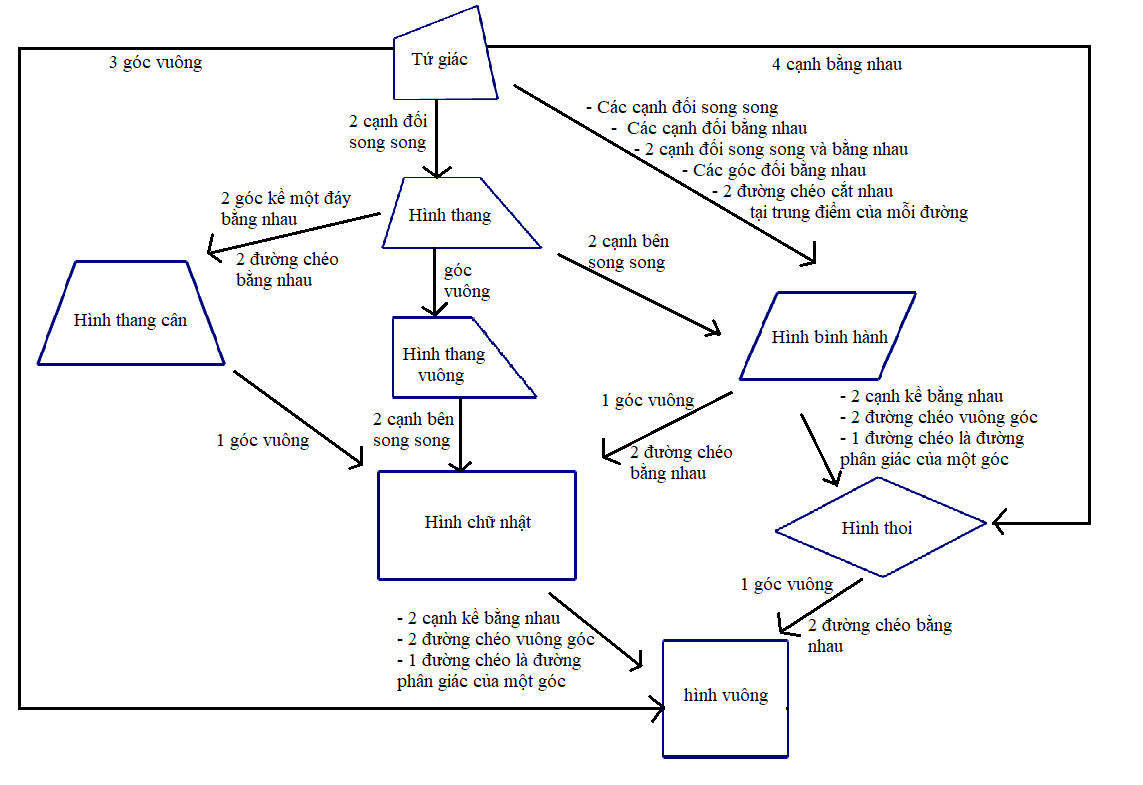
II. Bài tập

1.a) Cho tứ giác $ ABCD$ có $ \widehat{A}={{120}^{o}};\widehat{B}={{80}^{o}};\widehat{C}={{110}^{o}}.$ Tính $ \displaystyle \widehat{D}$

b) Cho hình thang vuông ABCD có $ \widehat{A}=\widehat{D}={{90}^{o}}$; AD = AB = 2cm. DC = 4cm. Tính $ \widehat{B},\widehat{C}$

2.Cho tam giác ABC vuông tại A có AB = 8cm; AC = 6cm. Gọi M, N lần lượt là trung điểm AB, AC.

a)     Tính độ dài NM;

b)    Gọi K là trung điểm BC. Tính độ dài AK.

3.a) Cho hình thang ABCD ( AB // CD). Gọi E, F lần lượt là trung điểm của AD và BC. Biết AB = 8cm; CD = 12cm. Tính độ dài EF.

b) Cho hình thang ABCD (AB // CD). Gọi E, F lần lượt là trung điểm của AD và BC. Biết AB = 10cm; EF = 16cm. Tính độ dài CD

4.a) Tính độ dài đường chéo hình chữ nhật ABCD có AB = 16cm; AD = 12cm

b) Tính cạnh và chu vi của hình thoi ABCD có độ dài đường chéo AC = 16cm; BD = 12cm

c) Tính cạnh và chu vi của hình vuông ABCD có độ dài đường chéo AC = 6cm

d) Tính độ dài đường chéo của hình vuông ABCD có độ dài cạnh AB = 5cm

5.Cho tam giác ABC (AB < AC), đường cao AK. Gọi 3 điểm D, E, F lần lượt là trung điểm của AB, AC, BC.

a)     BDEF là hình gì? Vì sao?

b)    Chứng minh DEFK là hình thang cân.

6.Cho tam giác cân ABC (AB = AC). Gọi M, N, P theo thứ tự là trung điểm của AB, AC, BC. Cho Q là điểm đối xứng của P qua N. Chứng minh:

a.      PMAQ là hình thang                                       b. BMNC là hình thang cân

c.  ABPQ là hình bình hành                                 d. AMPN là hình thoi

e.  APCQ là hình chữ nhật

7.Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng:

a)     $ \Delta ABE=\Delta CDF$

b)    Tứ giác DEBF là hình bình hành

c)     Các đường thẳng EF, DB và AC đồng quy

8.Cho hình bình hành ABCD có AB = 2AD ; E và F theo thứ tự là trung điểm của AB và CD.

a)     Các tứ giác AEFD, AECF là hình gì ? Vì sao?

b)    Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh tứ giác EMFN là hình chữ nhật

c)     Chứng minh các đường thẳng AC, BD, EF, MN đồng quy.

9.Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ A đến BD. Gọi M và N theo thứ tự là trung điểm của AH và DH.

a)     Chứng minh MN // AD

b)    Gọi I là trung điểm của BC. Chứng minh tứ giác BMNI là hình bình hành.

c)     Tính số đo góc ANI?

10.Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC; K là điểm đối xứng với M qua điểm I.

a)     Chứng minh tứ giác AMCK là hình chữ nhật.

b)    Tứ giác ABM là hình gì? Vì sao?

c)     Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh tứ giác ABEC là hình thoi.

d)    Tìm điều kiện $ \Delta ABC$ để tứ giác AMCK là hình vuông

11.Cho tam giác ABC vuông tại A, đường cao AH. D và E lần lượt là chân đường vuông góc hạ từ H xuống AB và AC.

a.      Chứng minh DE = AH

b.     Gọi M, N lần lượt là trung điểm của BH, HC. Chứng minh DMNE là hình thang vuông

c.      Cho BH = 4cm; HC = 9cm; AH = 6cm. Tính diện tích hình thang DMNE.

12.Cho tam giác ABC vuông tại A có BC = 2AB. Gọi M là trung điểm của BC. Nối A với M, trên tia đối của tia MA lấy điểm K sao cho AM = MK.

a)     Chứng minh rằng: Tứ giác ABKC là hình chữ nhật

b)    Gọi E là trung điểm của AM, F là điểm đối xứng với B qua E. Chứng minh tứ giác ABMF là hình thoi.

c)     Chứng minh MF // CK

d)    Chứng minh AC = KF

13.Cho $ \Delta ABC$ cân tại A, đường cao AH. Gọi D, E lần lượt là trung điểm của AB, AC.

a)     Chứng minh: DECH là hình bình hành

b)    Chứng minh: BCED là hình thang cân.

c)     Gọi F là điểm đối xứng của H qua E. Chứng minh: AHCF là hình chữ nhật.

d)    Gọi M là giao điểm DF và AE, N là giao điểm DC và HE. Chứng minh $ NM\bot DE$

14.Cho $ \Delta ABC$ cân tại A có đường trung tuyến AM. Gọi D là điểm đối xứng của A qua M.

a)     Chứng minh rằng tứ giác ABDC là hình thoi

b)    Gọi K là trung điểm của MC, E là điểm đối xứng của D qua K. Chứng minh rằng tứ giác AMKE là hình thang vuông

c)     AM và BE cắt nhau tại I. Chứng minh rằng I là trung điểm của BE.

d)    Chứng minh rằng AK, CI, EM đồng quy

15.Cho $ \Delta ABC$ vuông tại A (AB < AC), đường cao AH. Gọi D là điểm đối xứng với A qua H, M là điểm đối xứng với B qua H.

a)     Tứ giác ABDM là hình gì? Chứng minh?

b)    Biết AH = 2cm; BC = 5cm. Tính $ {{S}_{{BDC}}}$

c)     Chứng minh M là trực tâm của tam giác ADC.

d)    Gọi I là trung điểm của MC, N là giao điểm của DM và AC. Chứng minh $ \Delta NHI$ là tam giác vuông

16.Cho $ \Delta ABC$ vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC.

a)     Chứng minh tứ giác AHDE là hình chữ nhật.

b)    Gọi I là trung điểm của HB. Chứng minh DI vuông góc vơi DE.

c)     Gọi K là trung điểm của HC. Chứng minh IDEK là hình thang

d)    Giả sử DI = 1cm; EK = 4cm và AH = 4cm, tính diện tích tam giác ABC.

17.Cho $ \Delta ABC$ vuông tại A, trung tuyến AM. Gọi E và F lần lượt là hình chiếu của M lên AB và AC.

a)     Tứ giác AEMF là hình gì? Vì sao

b)    Gọi I là điểm đối xứng của M qua E. Chứng minh rằng: Tứ giác AMBI là hình thoi

c)     Chứng minh rằng: MI = AC

d)    Gọi K là điểm đối xứng của M qua F. Chứng minh rằng: BK, CI, AM đồng quy.

18.Cho $ \Delta ABC$ vuông tại A (AB < AC). M là trung điểm của BC. Vẽ MD vuông góc với AB tại D ; ME vuông góc với AC tại E.

a.      Chứng minh tứ giác ADME là hình chữ nhật.

b.     Chứng minh CMDE là hình bình hành.

c.      Vẽ AH vuông góc với BC. Chứng minh tứ giác MHDE là hình thang cân

d.     Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh H vuông góc với AC

19.Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm. Kẻ đường cao AH. Gọi D là điểm đối xứng với H qua AB, M là giao điểm của AB và HD, gọi E là điểm đối xứng với H qua AC, N là giao điểm của AC và HE. Chứng minh:

a)     Tam giác ABC vuông

b)    AH = MN

c)     D đối xứng với E qua A

d)    Gọi F là trung điểm BC. Chứng minh $ \displaystyle AF\bot MN$

20.Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB và E là điểm đối xứng với M qua D.

a.      Chứng minh rằng tứ giác AEBM là hình thoi

b.     Chứng minh rằng $ AB\bot EM$

c.      Gọi F là trung điểm của AM. Chứng minh rằng ba điểm E, F, C thẳng hàng.

21.Cho $ \Delta ABC$ vuông ở A ( AB < AC), đường cao AH. Gọi D là điểm đối xứng của A qua H. Đường thẳng kẻ qua D song song với AB cắt BC và AC lần lượt ở M và N. Chứng minh:

a)     Tứ giác ABDM là hình thoi.

b)    $ AM\bot CD$

c)     Gọi I là trung điểm của MC. Chứng minh tam giác HNI là tam giác vuông

22.Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.

a)     Chứng minh MD // AC

b)    Tứ giác AEBM là hình gì? Vì sao?

c)     Chứng minh AE = MC

d)    Cho AB = 3cm; BC = 5cm. Tính diện tích tam giác ABM?

Bồi dưỡng Toán 8, Hình học 8 - Tags: , ,