Dạng bài tập chứng minh quan hệ chia hết – Số học 6
Ở bài viết này, Timgiasuhanoi.com sẽ cùng các em học sinh lớp 6 đi làm những bài tập về dạng chứng minh quan hệ chia hết với việc áp dụng nguyên lý Dirich- le.
Trước tiên các em cần ghi nhớ lý thuyết:
Phương pháp chứng minh một số chia hết cho một số:
Để chứng minh A(n) chia hết cho một số m ta phân tích A(n) thành nhân tử có một nhân tử làm hoặc bội của m, nếu m là hợp số thì ta lại phân tích nó thành nhân tử có các đôi một nguyên tố cùng nhau, rồi chứng minh A(n) chia hết cho các số đó.
Và lưu ý một số chú ý dưới đây:
+ Với k số nguyên liên tiếp bao giờ cũng tồn tại một bội của k
+ Khi chứng minh A(n) chia hết cho m ta xét mọi trường hợp về số dư khi chia A(n) cho m
+ Với mọi số nguyên a, b và số tự nhiên n thì:
- an – bn chia hết cho a – b (a – b)
- a2n + 1 + b2n + 1 chia hết cho a + b
- (a + b)n = B(a) + bn
- (a + 1)n là BS(a )+ 1
- (a – 1)2n là B(a) + 1
- (a – 1)2n + 1 là B(a) – 1
Với mỗi ví dụ sẽ có hướng phân tích đề bài và lời giải.
Ví dụ1. Chứng minh rằng:
A = n3(n2 -7)2 – 36n chia hết cho 5040 với mọi số tự nhiên n.
Hướng phân tích:
+ Trước hết cho hoc sinh nhận xét về các hạng tử của biểu thức A
+ Từ đó phân tích A thành nhân tử
Giải: Ta có
A =n[n2(n2 -7)2 -36]= n[(n3 -7n2)-36]
= n(n3 -7n2 -6)( n3 -7n2 +6)
Mà n3 -7n2 -6 = (n+1) (n+2) (n-3)
n3 -7n2 +6 = (n-1)(n-2)(n+3)
Do đó:
A= (n-3)(n-2)(n-1)(n+1)(n+2)(n+3)
Đây là tích của 7 số nguyên liên tiếp.Trong 7 số nguyên liên tiếp
+Tồn tại một bội của 5 ⇒ A chia hết cho 5
+Tồn tại một bội của 7 ⇒ A chia hết cho 7
+Tồn tại hai bội của 3 ⇒ A chia hết cho 9
+Tồn tại ba bội số của 2,trong đó có một bội số của 4 ⇒ A chia hết cho 16
A chia hết cho các số 5,7,9,16 đôi một nguyên tố cùng nhau nên A chia hết cho
5.7.9.16 =5040.
+ Qua ví dụ 1 rút ra cách làm như sau:
Gọi A(n) là một biểu thức phụ thuộc vào n (n ∈ N hoặc n ∈ Z).
Chú ý 1:
+Để chứng minh biểu thức A(n) chia hết cho một số, ta thường phân tích A(n) thành thừa số, trong đó có một thừa số là m.Nếu m là hợp số, ta phân tích nó thành môt tích các thừa số đôi một nguyên tố cùng nhau, rồi chứng minh A(n)chia hết cho tất cả các số đó.
+Trong quá trình chứng minh bài toán trên ta đã sử dụng các kiến thức của lớp 6 :
-Phân tích một số ra thừa số nguyên tố .
-Tính chất chia hết của một tích (thừa số là số nguyên tố )
-Nguyên lý Dirich- le
Lưu ý: Trong k số nguyên liên tiếp, bao giờ cũng tồn tại một bội số của k.
Ví dụ 2. Chứng minh rằng với moi số nguyên a thì
a) a2 -a chia hết cho 2.
b) a3 -a chia hết cho 3.
c) a5 -a chia hết cho 5.
d) a7 -a chia hết cho 7.
Giải:
a) a2 – a =a(a-1), chia hết cho 2.
b) a3 -a = a( a2 – 1) = a(a-1)(a+1), tích này chia hết cho 3 vì tồn tại một bội của 3.
+ Ở phần a, b học sinh dễ dàng làm được nhờ các bài toán đã quen thuộc
+ Để chứng minh a(a -1 ) chia hết cho 2, ta đã xét số dư của a khi chia cho 2 (hoặc dụng nguyên lý Dirich- le )
c) Cách 1
A = a5 -1= a(a2+1)(a2 -1)
Xét các trường hợp a = 5k, a= 5k ± 1, a=5k ± 2
+Ta vận dụng vào tính chia hết của số nguyên về xét số dư
suy ra A chia hết cho 5.
Cách 2.
A = a5 -1= a(a2+1)(a2 -1)
= a(a2+1)(a2 -4+5)
= a(a2+1)(a2 -4)+ 5a( a2 -1)
= (a -2) (a-1)a(a+1)(a+2) + 5a(a2 -1)
Số hạng thứ nhất là tích của năm số nguyên liên tiếp nên chia hết cho 5,số hạng thứ hai cũng chia hết cho 5.
Do đó A = a5 -1 chia hết cho 5.
+Ta vận dụng tính chia hết của một tổng vào giải .
+ Qua ví dụ 2 để chứng minh chia hết ta đã làm như sau:
Chú ý 2: Khi chứng minh A(n) chia hết cho m, ta có thể xét mọi trường hợp về số dư khi chia n cho m.
Ví dụ 3.
a)Chứng minh rằng một số chính phương chia hết cho 3 chỉ có thể có số dư bằng 0 hoặc 1.
b) Chứng minh rằng một số chính phương chia cho 4 chỉ có thể có số dư bằng 0 hoặc 1.
c)Các số sau có là số chính phương không?
M = 19922 + 19932 +19942
N = 19922 + 19932 +19942 +19952
P = 1+ 9100+ 94100 +1994100.
d)Trong dãy sau có tồn tại số nào là số chính phương không?
11, 111,1111,11111,…….
Giải: Gọi A là số chính phương A = n2 (n ∈ N)
a)Xét các trường hợp:
n= 3k (k ∈ N) ⇒ A = 9k2 chia hết cho 3
n= 3k 1 (k ∈ N) A = 9k2 6k +1 chia cho 3 dư 1
Vậy số chính phương chia cho 3 chỉ có thể có số dư bằng 0 hoặc 1.
+Ta đã sử tính chia hết cho 3 và số dư trong phép chia cho 3 .
b)Xét các trường hợp
n =2k (k ∈ N) ⇒ A= 4k2, chia hết cho 4.
n= 2k+1(k ∈ N) ⇒ A = 4k2 +4k +1
= 4k(k+1)+1,
chia cho 4 dư 1(chia cho 8 cũng dư 1)
vậy số chính phương chia cho 4 chỉ có thể có số dư bằng 0 hoặc 1.
+Ta đã sử tính chia hết cho 4 và số dư trong phép chia cho 4 .
Chú ý: Từ bài toán trên ta thấy:
-Số chính phương chẵn chia hết cho 4
-Số chính phương lẻ chia cho 4 dư 1( chia cho 8 cũng dư 1).
c) Các số 19932,19942 là số chính phương không chia hết cho 3 nên chia cho 3 dư 1,còn 19922 chia hết cho 3.
Vậy M chia cho 3 dư 2,không là số chính phương.
Các số 19922,19942 là số chính phương chẵn nên chia hết cho 4.
Các số 19932,19952 là số chính phương lẻ nên chia cho 4 dư 1.
Vậy số N chia cho 4 dư 2,không là số chính phương.
+Ta đã vận dụng tính chất chia hết của số chính phương và xét số dư cửa các số chính phương đó khi các số đó chẳn hay lẻ .
d) Mọi số của dãy đều tận cùng là 11 nên chia cho 4 dư 3.Mặt khác số chính phương lẻ thì chia cho 4 dư 1.
Vậy không có số nào của dãy là số chính phương.
Chú ý 3: Khi chứng minh về tính chất chia hết của các luỹ thừa,ta còn sử dụng các hằng đẳng thức bậc cao và công thức Niu-tơn sau đây:
+an -bn =(a-b)(an-1+an-2b+an-3b2+…+abn-2+bn-1) (1)
+an+bn=(a+b)(an-1-an-2b+an-3b2-…-abn-2+bn-1) (2)
với mọi số lẻ n.
Công thức Niu-tơn
(a+b)n= an+c1an-1b+c2an-2b2+…+cn-1abn-1+bn
Trong công thức trên, vế phải là một đa thức có n+1 hạng tử, bậc của mỗi hạng tử đối với tập hợp các biến là a,b là n.Các hệ số c1,c2,…cn-1 được xác định bởi tam giác Pa -xcan:
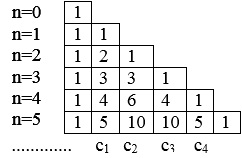
Áp dụng các hằng đẳng thức trên vào tính chia hết, ta có với mọi số tự nhiên a,b và số tự nhiên n :
an -bn chia hết cho a-b (a ≠ b)
a2n+1 +b2n+1 chia hết cho a+b ( a ≠-b)
(a+b)n =Bs a+bn (Bs a là bội của a).
Đặc biệt chú ý đến:
(a+1)n = Bs( a +1)
( a -1)n = Bs (a- 1)
(a-1)2n+1= Bs( a – 1)
*Tất cả các công thức Niu Tơn trên chỉ áp dụng cho học sinh các khối 8 , 9 .
Ví dụ 4. Chứng minh rằng với mọi số tự nhiên n, biểu thức 16n -1 chia hết cho 17 khi và chỉ khi n là số chẵn.
Giải:
Cách 1:
Nếu n chẵn (n=2k, kN) thì
A= 162k -1 = (162)k -1 chia hết cho 162 -1
Theo hằng đẳng thức (1)
Mà 162 -1 =255 chia hết cho 17.
Vậy A chia hết cho 17
Nếu n lẻ thì A = 16n +1 -2,
mà 16n+1 chia hết cho 17 theo hằng đẳng thức (9),nên A không chia hết cho 17
vậy A chia hết cho 17 n chẵn.
Cách 2: A=16n -1 =(17-1)n -1
= B (17) +(-1)n -1(theo công thức Niu-tơn)
Nếu n chẵn thì A =B (17) +1-1 =B (17)
Nếu n lẻ thì A = B (17) -1 -1 = B (17 )-2
Không chia hết cho 17.
Chú ý 4: Người ta còn dùng phương pháp phản chứng,nguyên lý Di ríchlet để chứng minh quan hệ chia hết.
Ví dụ 5. Chứng minh rằng tồn tại một bội số của 2003 có dạng
2004 2004 …….2004
Giải: Xét 2004 số :
A1 =2004
A2 =2004 2004
…
A2004=2004 2004….2004 (Nhóm 2004 có mặt 2004 lần).
Theo nguyên lý Dirich let, tồn tại hai số có cùng số dư khi chia cho 2003.
Gọi hai số đó là am và an (1nm2004)
Thì am -an chia hết cho 2003.Ta có
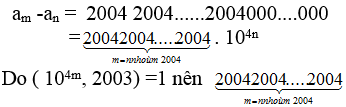
Chia hết cho 2003.
Bài tập tương tự:
Bài 1. Chứng minh rằng n6 + n4 – 2n2 chia hết cho 72 với mọi số nguyên n.
Giải:
Ta có n6 + n4 – 2n2
= n2 ( n4 +n2 – 2)
=n2 (n4 -1 + n2 -1 )
= n2 [ (n2 -1)(n2 +1) +(n2 -1)]
= n2 (n-1)(n+1)(n2 +2)
+Xét các trường hợp n= 2k, n=2k+1
n6 + n4 – 2n2 $ \displaystyle \vdots $ 8
+Xét các trường hợp n = 3a, n=3a ± 1
n6 + n4 – 2n2 $ \displaystyle \vdots $ 9
vậy n6 + n4 – 2n2 $ \displaystyle \vdots $ 72 với mọi số nguyên n
Bài 2. Chứng minh rằng 32n -9 chia hết cho 72 với mọi số nguyên dương n
Giải:
Ta có B =32n -9= 9n – 9,nên B chia hết cho 9
Mặt khác B = 32n – 9 = (3n -1)(3n +1) -8
Do 3n -1,3n +1 là hai số chẵn liên tiếp nên B chia hết cho 8
Vậy B $ \displaystyle \vdots $ 72
* Bài tập tự làm
Chứng minh rằng:
1. n3+6n2+8n chia hết cho 48 với mọi n chẵn
2. n4-10n2+9 chia hết cho 384 với mọi số n lẻ