Dạng 1: Rút gọn biểu thức
I/ Biểu thức số học
Phương pháp:
Dùng các Phương pháp biến đổi căn thức (đưa ra ; đưa vào; ;khử; trục; cộng,trừ căn thức đồng dạng; rút gọn phân số…) để rút gọn biểu thức.
Bài tập: Thực hiện phép tính:
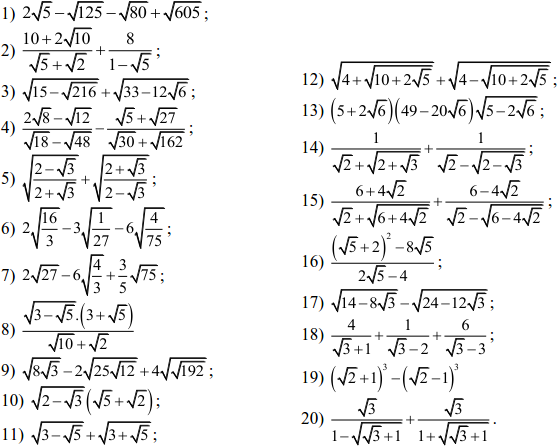
II/ Biểu thức đại số:
Phương pháp:
– Phân tích đa thức tử và mẫu thành nhân tử;
– Tìm ĐKXĐ (Nếu bài toán chưa cho ĐKXĐ)
– Rút gọn từng phân thức(nếu được)
– Thực hiện các phép biến đổi đồng nhất như:
+ Quy đồng(đối với phép cộng trừ) ; nhân ,chia.
+ Bỏ ngoặc: bằng cách nhân đơn ; đa thức hoặc dùng hằng đẳng thức
+ Thu gọn: cộng, trừ các hạng tử đồng dạng.
+ Phân tích thành nhân tử – rút gọn
Chú ý: – Trong mỗi bài toán rút gọn thường có các câu thuộc các loại toán: Tính giá trị biểu thức; giải Phương trình; bất Phương trình; tìm giá trị của biến để biểu thức có giá trị nguyên; tìm giá trị nhỏ nhất ,lớn nhất…Do vậy ta phải áp dụng các Phương pháp giải tương ứng, thích hợp cho từng loại bài.

Bài tập:
Bài 1: Cho biểu thức
a. Rút gọn biểu thức A;
b. Tìm giá trị của x để A > – 6.

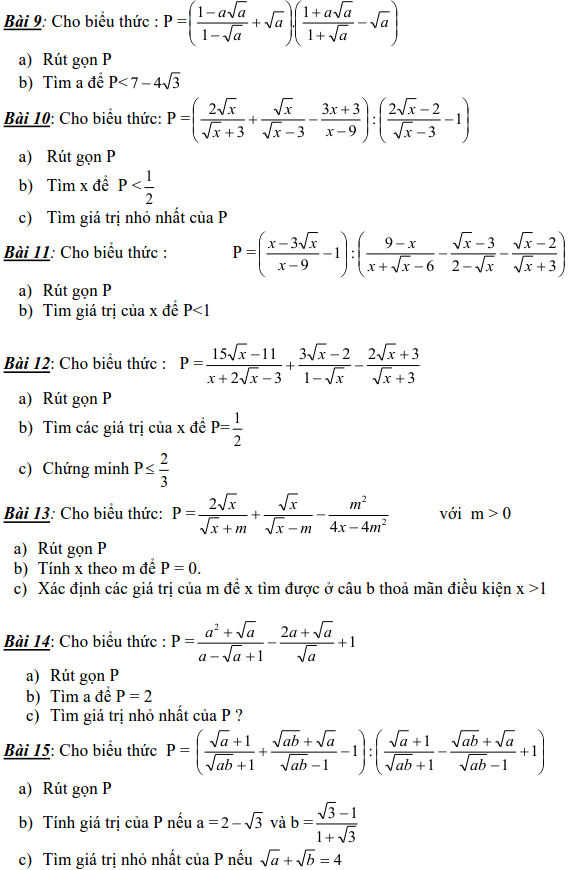
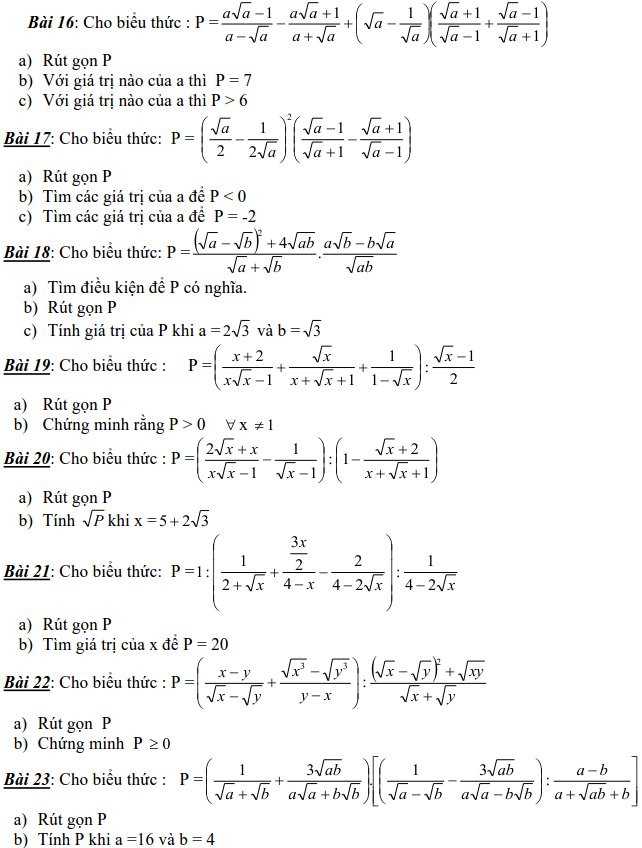
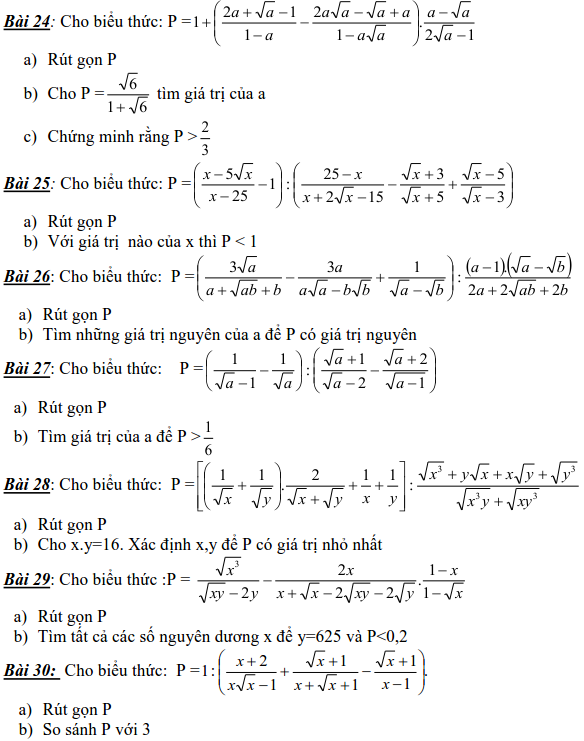
Các dạng phương trình nghiệm nguyên và cách giải
Sử dụng phương pháp hình học để tìm GTLN, GTNN
Sử dụng phương pháp xét từng khoảng giá trị để tìm GTLN, GTNN
Sử dụng phương pháp miền giá trị để tìm GTLN, GTNN
Sử dụng biểu thức phụ để tìm để tìm GTLN, GTNN
Sử dụng phương pháp đặt biến phụ để tìm GTLN, GTNN
Sử dụng các bất đẳng thức cơ bản để tìm GTLN, GTNN