Cách chứng minh hai góc bằng nhau, hai đoạn thẳng bằng nhau qua ví dụ
Ví dụ 1: Cho ΔABC có 3 góc nhọn (AB < AC), M là trung điểm của AC. Trên tia đối của tia MB lấy điểm D sao cho BM = MD.
a) Chứng minh ΔABM = ? CDM
b) Chứng minh AB // CD.
c) Vẽ AH, CK vuông góc với BD (K, H thuộc BD). Chứng minh BH = DK
Giải.
a) Chứng minh : ?ABM = ?CDM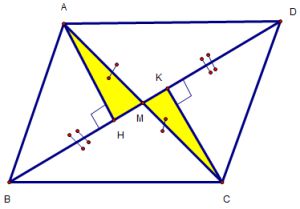
Xét ?ABM và ?CDM :
MA = MC (gt)
MB = MD (gt)
(đối đinh)
=> ?ABM = ?CDM (c – g – c)
b) Chứng minh : AB // CD
Ta có :
(góc tương ứng của ?ABM = ?CDM)
Mà : ở vị trí so le trong
Nên : AB // CD
c) Chứng minh BK = DH
Xét ?ABH và ?CDK, ta có :
(cmt)
AB = CD (?ABM = ?CDM)
=> ?ABH = ?CDK (cạnh huyền – góc nhọn)
=> BH = CK (cạnh tương ứng)
Ví dụ 2:
Cho ΔABC vuông tại A, có góc B = 55°
a) Tính số đo của góc ACB
b) Trên tia đối của tia AC lấy điểm D sao cho AD = AC. Chứng minh: ΔABC = ΔABD.
c) Từ D vẽ đường thẳng song song với BC và cắt tia BA tại E. Chứng minh: ΔDAB = ΔDAE.
d) Qua C vẽ đường thẳng a vuông góc với AC và cắt tia DE tại K. Chứng minh E là trung điểm của đoạn thẳng DK.
Giải.
a) Tính góc ACB :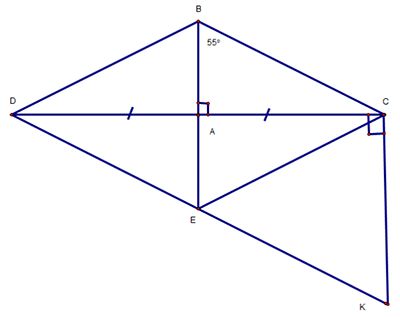
trong tam giác ABC, ta có :
=>
b) cm : ΔABC = ΔABD
Xét ΔABC và ΔABD, ta có :
AB cạnh chung.
AC = AD (gt)
=> ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
c) cm : ΔDAB = ΔDAE
ta có :
(ΔABC = ΔABD)
(so le trong)
=>
Xét ΔDAB VÀ ΔDAE, ta có :
(cmt)
AD cạnh chung
=> ΔDAB = ΔDAE (cạnh góc vuông – góc nhọn)
d) E là trung điểm DK
Xét ΔCAB VÀ ΔDAE, ta có :
(so le trong)
AB = AE (ΔDAB = ΔDAE)
=> ΔCAB = ΔDAE
=> DE = BC (1)
TA CÓ : AE vuông góc AC (gt) và KC vuông góc AC (gt)
=> AE // CK
=> (so le trong)
Xét ΔCEB VÀ ΔEKC, ta có :
(cmt)
EC cạnh chung
(so le trong)
=> ΔCEB = ΔEKC (g – c – g)
=> KE = BC (2)
từ (1) và (2), ta có :
DE = BC (cmt) và KE = BC (cmt)
=> DE = EK
hay E là trung điểm DK
Cách chứng minh 3 điểm thẳng hàng qua các ví dụ – Toán lớp 7
Định nghĩa, tính chất ba đường cao của tam giác
Tính chất đường trung trực của một đoạn thẳng
Quan hệ giữa ba cạnh của một tam giác, bất đẳng thức tam giác
Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Quan hệ giữa góc và cạnh đối diện trong một tam giác
Định lí Pitago trong tam giác vuông