Cách chứng minh 3 điểm thẳng hàng qua các ví dụ – Toán lớp 7

Bài viết này hướng dẫn cho các em cách chứng minh 3 điểm thẳng hàng qua các ví dụ có lời giải chi tiết, dễ hiểu.

Sau mỗi ví dụ là nhận xét về hướng giải quyết một bài toán chứng minh 3 điểm thẳng hàng.
Ví dụ 1 : Cho D ABC vuông tại B. Trên nữa mặt phẳng bờ BC không có điểm A, vẽ tia Cx vuông góc BC. Trên tia Cx lấy M sao cho CM = AB. Chứng minh A, M và D là trung điểm của BC thẳng hàng.

Giải.

Xét ?ABD và ?MCD, ta có :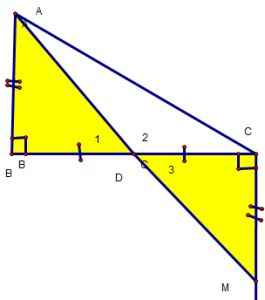Cách chứng minh 3 điểm thẳng hàng qua các ví dụ - Toán lớp 7-1

\widehat{B} =\widehat{C}=90^0

AB = CM (gt)

DB = DC (D là trung điểm của BC)

=> ?ABD = ?MCD (2 cạnh góc vuông)
=> \widehat{D_1} =\widehat{D_3}
Mặt khác : \widehat{D_1} +\widehat{D_2}=180^0 (B, D, C thẳng hàng)
=>\widehat{D_2} +\widehat{D_3}=180^0
Hay : \widehat{ADM} =180^0
=> A, D, M thẳng hàng ( góc bẹt)
Nhận xét: Ở bài này chứng minh 3 điểm thẳng hàng bằng cách chứng minh cho góc tạo bởi 3 điểm đó là 180 độ.

Ví dụ 2 : Cho tam giác ABC . gọi D, E lần lượt  là trung điểm của AB, AC. Trên tia đối của tia DC, lấy điểm M sao cho MD = CD. Trên tia đối của tia EB, lấy điểm N sao cho EN = BE. chứng minh :  A là trung điểm của MN.

GIẢI.

Xét ΔBCD và ΔBMD, ta có :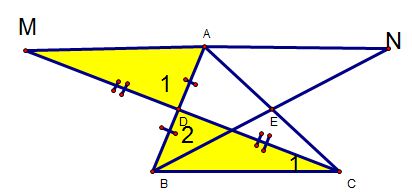Cách chứng minh 3 điểm thẳng hàng qua các ví dụ - Toán lớp 7-2

 DB = DA (D là trung điểm của AB)

\widehat{D_1}=\widehat{D_2} (đối đỉnh).

DC  = DM (gt).

=> ΔBCD = ΔBMD (c -g -c)
=>\widehat{C_1}=\widehat{M} và BC = AM.
Mà : \widehat{C_1}; \widehat{M} ở vị trí so le trong. => BC // AM.
Chứng minh tương tự,
ta được : BC // AN và BC = AN.
ta có : BC // AM (cmt) và BC // AN (cmt)
=> A, M. N thẳng hàng. (1)
BC = AM và BC = AN => AM = AN (2).
Từ (1) và (2), suy ra : A là trung điểm của MN.
Nhận xét: Chứng minh 3 điểm A, M, N thẳng hàng trước, sau đó chứng minh AM = AN

Ví dụ 3 :
Cho tam giác ABC vuông góc tại A có góc B  = 530.
a) Tính góc C.
b) Trên cạnh BC, lấy điểm D sao cho BD = BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. cmr : ΔBEA = ΔBED.
c) Qua C, vẽ đường thẳng vuông góc với BE tại H. CH cắt đường thẳng AB tại F. cm : ΔBHF = ΔBHC.
d) Cmr : ΔBAC = ΔBDF và D, E, F thẳng hàng.

Giải.

a. Tính góc C :
Xét ΔBAC, ta có :
\widehat{A} +\widehat{B} +\widehat{C} =180^0
=> \widehat{C} =180^0-(\widehat{A} +\widehat{B})
=>  \widehat{C} =180^0-(90^0+53^0)=37^0
b. ΔBEA = ΔBED :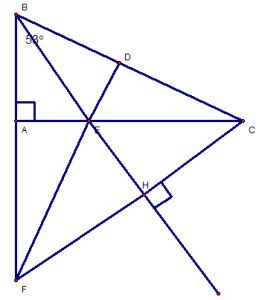Cách chứng minh 3 điểm thẳng hàng qua các ví dụ - Toán lớp 7-3
Xét ΔBEA và ΔBED, ta có :

BE cạnh chung.

\widehat{ABE} =\widehat{DBE} (BE là tia phân giác của góc B)

BD = BA (gt)

=> ΔBEA = ΔBED (c – g – c)
c. ΔBHF = ΔBHC
Xét ΔBHF và ΔBHC, ta có :

BH cạnh chung.

\widehat{ABH} =\widehat{DBH} (BE là tia phân giác của góc B)

\widehat{BHF} =\widehat{BHC}=90^0  (gt)

=> ΔBHF = ΔBHC (cạnh huyền – góc nhọn)
=> BF = BC (cạnh tương ứng)
d. ΔBAC = ΔBDF và D, E, F thẳng hàng
xét ΔBAC và ΔBDF, ta có:

BC = BF (cmt)

Góc B chung.

BA = BC (gt)

=> ΔBAC = ΔBDF
=> \widehat{BAC} =\widehat{BDF}
Mà : \widehat{BAC} =90^0 (gt)
Nên : \widehat{BDF} =90^0 hay BD \bot DF (1)
Mặt khác : \widehat{BAE} =\widehat{BDF}  (hai góc tương ứng của  ΔBEA = ΔBED)

Mà : \widehat{BAE} =90^0 (gt)

Nên : \widehat{BDE} =90^0 hay BD \bot DE (2)

Từ (1) và (2), suy ra : DE trùng DF
Hay : D, E, F thẳng hàng.

Bài tập tự giải:

Ví dụ 1 : Cho tam giác ABC . Trên tia đối của tia AB lấy điểm F sao cho AB = FA. Trên tia đối của tia AC lấy điểm E sao cho AC = AE.
a) Chứng minh: Δ EAF = Δ CAB
b)Gọi K là trung điểm EF và D là trung điểm BC. Chứng minh : KB = FD.
d) Chứng minh: K, A, D thẳng hàng.
Ví dụ 2 :Cho Δ ABC có M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D sao cho MD = MC.
a) Chứng minh Δ MAD = Δ MBC và AD // CB.
b) Lấy N thuộc AD; NM cắt BC tại P. Chứng minh AN = BP.
c) Trên nửa mặt phẳng bờ AB không chứa điểm D, vẽ tia AE sao cho góc EAB + góc ABC = 180^0 . Chứng tỏ D, A, E thẳng hàng.

Hình học 7 - Tags: ,