Cách chứng minh 2 mặt phẳng song song trong không gian

Các cách chứng minh hai mặt phẳng song song trong không gian qua các ví dụ minh họa có lời giải chi tiết và bài tập rèn luyện.

Định nghĩa: Hai mặt phẳng gọi là song song nếu chúng không có điểm chung.

Điều kiện song song của hai mặt phẳng:

Nếu mặt phẳng $(P)$ chứa hai đường thẳng $a$ và $b$ cắt nhau và cùng song song với mặt phẳng $(Q)$ thì $(P)$ song song với $(Q)$

$\begin{array}{l}a\text{ và }b\subset (P)\\ a\text{ cắt }b\\ a,b//(Q)\end{array}\}\Rightarrow (P)//(Q)$

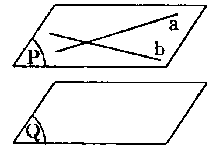
Các định lí:

a) Qua một điểm nằm ngoài mặt phẳng có một và chỉ một mặt phẳng song song mặt phẳng đó.

b) Nếu đường thẳng $a$ song song mặt phẳng $(Q)$ thì qua $a$ chỉ có duy nhất một mặt phẳng song song mặt phẳng $(Q)$.

c) Nếu hai mặt phẳng $(P)$ và $(Q)$ song song thì mọi mặt phẳng $(R)$ cắt $(P)$ thì cắt $(Q)$ và các giao tuyến của chúng song song.

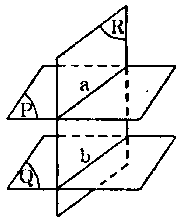
d) Hai mặt phẳng phân biệt cùng song song với một mặt phẳng thì chúng song song với nhau.

e) Hai mặt phẳng song song chắn trên hai cát tuyến song song những đoạn bằng nhau.

f) Định lí Thales:

Ba mặt phẳng song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ.

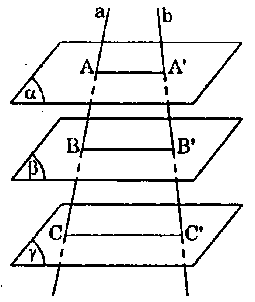
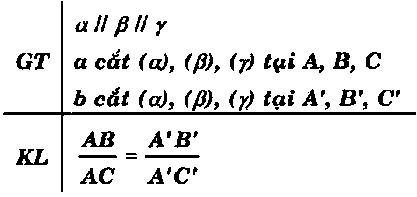
g) Định lí Thales đảo:

Nếu trên hai đường thẳng chéo nhau $a$ và $b$ lần lượt lấy các điểm $A,B,C$  và $A^{\prime },B^{\prime },C^{\prime }$ sao cho $\frac{AB}{A^{\prime }{B}^{\prime }}=\frac{BC}{B^{\prime }{C}^{\prime }}=\frac{AC}{A^{\prime }{C}^{\prime }}$ thì ba đường thẳng $A{A}^{\prime },B{B}^{\prime },C{C}^{\prime }$ lần lượt nằm trên ba mặt phẳng song song.

Ví dụ minh họa:

Bài tập chứng minh 2 mặt phẳng song song

• Cách chứng minh 2 đường thẳng song song trong không gian

• 30 câu trắc nghiệm Phép tịnh tiến có lời giải – Toán lớp 11

• Tổng hợp kiến thức cơ bản Toán lớp 11 – Nguyễn Thanh Nhàn

• Lý thuyết khái niệm về phép dời hình và hai hình bằng nhau

• Cách tính khoảng cách giữa 2 đường thẳng chéo nhau trong không gian

• Tổng hợp các chuyên đề Toán lớp 11

• 30 câu trắc nghiệm cấp số cộng, cấp số nhân có đáp án