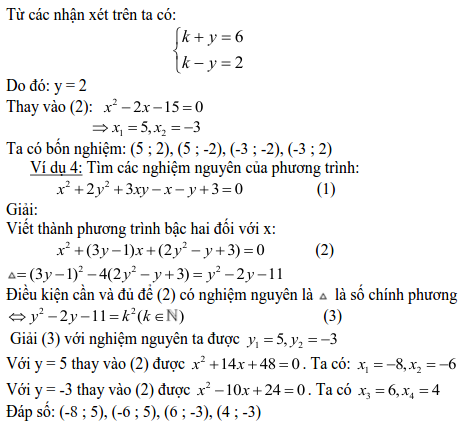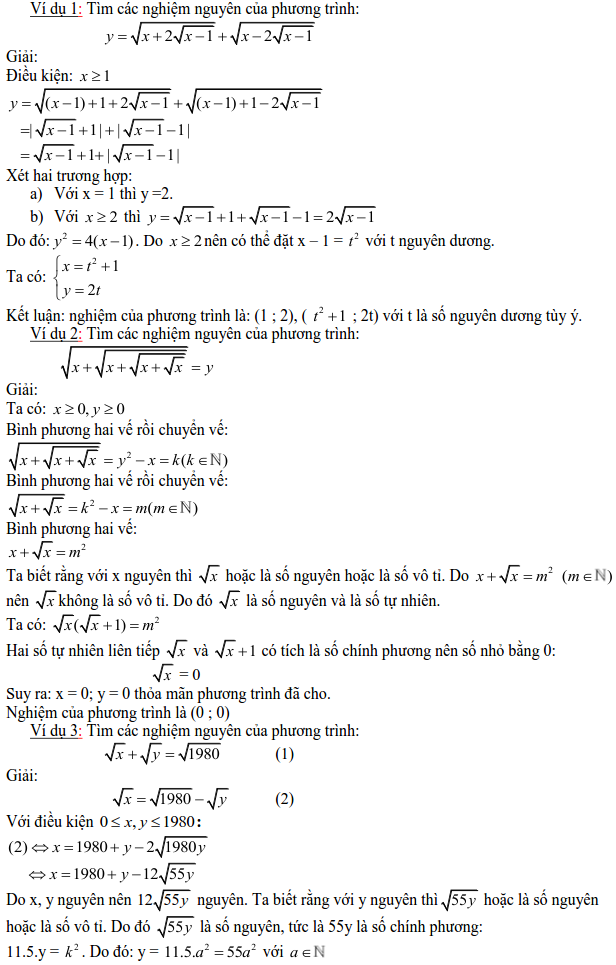Các dạng phương trình nghiệm nguyên và cách giải
Các bài tập về phương trình nghiệm nguyên thường xuất hiện trong đề thi học sinh giỏi, đề thi tuyển sinh vào 10 môn Toán.
Và nó chỉ xoay quanh các dạng mà Timgiasuhanoi.com đưa ra dưới đây.
Cách giải các dạng phương trình nghiệm nguyên:
1. Phương trình bậc nhất hai ẩn ax + by = c (*) trong đó a,b nguyên khác 0
2. Phương trình bậc nhất ba ẩn
3. Phương trình bậc hai hai ẩn
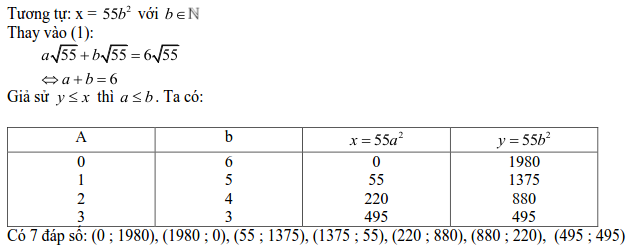
4. Phương trình chứa căn thức
5. Bài tập tìm nghiệm nguyên của phương trình
Sử dụng phương pháp hình học để tìm GTLN, GTNN
Sử dụng phương pháp xét từng khoảng giá trị để tìm GTLN, GTNN
Sử dụng phương pháp miền giá trị để tìm GTLN, GTNN
Sử dụng biểu thức phụ để tìm để tìm GTLN, GTNN
Sử dụng phương pháp đặt biến phụ để tìm GTLN, GTNN
Sử dụng các bất đẳng thức cơ bản để tìm GTLN, GTNN
Sử dụng phép biến đổi đồng nhất để tìm cực trị (GTLN, GTNN)