Các dạng bài tập Toán lớp 5 ôn hè lên 6

Ôn tập hè từ lớp 5 lên lớp 6 với các dạng bài tập: phép toán với phân số, Tìm x, Tính nhanh, Đổi đơn vị đo, Tính diện tích, Chuyển động…

Tất cả đều là bài tập toán tự giải. Bài nào khó cần trợ giúp các bạn có thể comment bên dưới.

I. Các phép toán với số thập phân

Bài 1: Đặt tính rồi tính

a) $ 247,06+316,492$

$ 201,4-78,55$

$ 37,14\times 82$

$ 345,6:72$

b. $ 78,27+39,18$

$ 89,32-37,639$

$ 3,18\times 5,24$

$ 99,3472:32,68$

Bài 2: Tính

a) $ 33,76+19,52+6,24$

b) $ \left( {27,09+258,91} \right)\times 25,4$

c) $ 31,5\times 2,6+39,72$

d) $ \left( {128,4-73,2} \right):2,4+18,32$

e) $ 38,4+13,05:1,5-25,17$

II. Toán tìm x

Bài 1: Tìm x

a) $ x+9,44=18,36$

b) $ x-5,2=1,9+3,8$

c) $ 7,9-x=2,5$

d) $ x+2,7=8,7+4,9$

e) $ 52\times \left( {x:78} \right)=3380$

f) $ x:5,12=3,7$

g) $ 1,36\times x=4,08\times 4,76$

h) $ x\times 0,34=1,19\times 1,02$

i) $ x+1,27=13,5:4,5$

j) $ x:2+x+x:3+x:4=25$

III. Toán tính nhanh

Bài 1: Tính nhanh

a) $ \frac{{6\times 7\times 8\times 9\times 10}}{{20\times 18\times 16\times 14\times 12}}$

b) $ \frac{1}{{10000}}+\frac{{13}}{{10000}}+\frac{{25}}{{10000}}+…+\frac{{97}}{{10000}}+\frac{{109}}{{10000}}$

c) $ \frac{4}{3}\times 2019\times 0,75$

d) $ 1,27+2,77+4,27+5,77+7,27+8,77+10,27+11,77+13,27+14,77$

e) $ 4\times 5\times 0,25\times \frac{1}{5}\times \frac{1}{2}\times 2$

f) $ \frac{{2003\times 1999-2003\times 999}}{{2004\times 999+1004}}$

Bài 2: Tính bằng cách thuận tiện

a) $ 60-26,75-13,25$

b) $ 38,25-18,25+21,64-11,64+9,93$

c) $ 45,28+52,17-15,28-12,17$

d) $ \left( {72,69+18,47} \right)-\left( {8,47+22,69} \right)$

e) $ 64\times 23+37\times 23-23$

f) $ 4,86\times 0,25\times 40$

g) $ 6,498\times 825,87+6,498\times 174,13$

h) $ 0,8\times 96+1,6\times 2$

i) $ 96,28\times 3,527+3,527\times 3,72$

f) $ 8\times 4\times 125\times 25$

IV. Đổi đơn vị đo

Bài 1: Viết các số thích hợp vào chỗ chấm

a) $ 1\frac{1}{4}$ giờ = ………. giờ ………. phút 182 phút = ……… giờ ……… phút

2,5 giờ = ………. phút 1,5 giờ = ………. phút

6 ngày 8 giờ = ………. giờ 3 nằm rưỡi = ………. tháng

$ \frac{3}{4}$ giờ = ………. phút 75 giây = ………. phút ………. giây

215 phút = ………. giờ ………. phút $ 1\frac{2}{5}$ giờ = ………. phút

b) 4 tấn 52 yến = ………. kg 35 kg 23g = ………. kg

2 tấn 135kg = ………. tấn 520g = ………. kg

21 tấn 6kg = ………. tấn 2kg 30g = ………. kg

45kg 23g = ………. kg 20kg 3g = ………. kg

72000 yến = ………. tấn 3206g = ………. kg ………. g

c) 60dm 3cm = ………. dm 14m 7cm = ………. m

315cm = ………. m 246cm = ………. m

3km 245m = ………. km 34dm = ………. m

386cm = ………. m 5km 34m = ………. km

197m = ………. km 3km 245m = ………. km

d) $ 3{{m}^{2}}$ $ 5d{{m}^{2}}$ = ………. $ {{m}^{2}}$ $ 42d{{m}^{2}}=……….\,\,{{m}^{2}}$

$ 56d{{m}^{2}}$ = ………. $ {{m}^{2}}$ $ 17d{{m}^{2}}$ $ 23c{{m}^{2}}$ = ……….$ d{{m}^{2}}$

$ 23c{{m}^{2}}$ = ………. $ d{{m}^{2}}$ $ 4{{m}^{2}}$ $ 3d{{m}^{2}}$ = ………. $ {{m}^{2}}$

$ 2c{{m}^{2}}$ $ 5m{{m}^{2}}$ = ………. $ \displaystyle c{{m}^{2}}$ $ 37d{{m}^{2}}$ = ………. $ {{m}^{2}}$

$ 123,9ha$ = ………. $ k{{m}^{2}}$ $ 36,9d{{m}^{2}}$ = ………. $ {{m}^{2}}$

$ 30000{{m}^{2}}=……….\,\,ha$ $ 95k{{m}^{2}}=……….\,\,h{{m}^{2}}$

e) $ 15d{{m}^{3}}\,\,53c{{m}^{3}}=………..\,\,c{{m}^{3}}$ $ 52{{m}^{3}}\,\,45d{{m}^{3}}=……….\,\,d{{m}^{3}}$

$ 7,54{{m}^{3}}=……….\,\,c{{m}^{3}}$ $ 78{{m}^{3}}\,\,5d{{m}^{3}}=……….\,\,{{m}^{3}}$

$ \frac{3}{4}{{m}^{3}}=……….\,\,d{{m}^{3}}$ $ \frac{1}{4}d{{m}^{3}}=……….\,\,c{{m}^{3}}$

$ 4380c{{m}^{3}}=……….\,\,d{{m}^{3}}$ $ 78,9{{m}^{3}}=……….\,\,d{{m}^{3}}$

V. Hình học

1. Diện tích tam giác, hình thang, hình tròn

Bài 1: Cho $ \Delta ABC$ có chiều cao $ AH=25cm,$ diện tích là $ 200c{{m}^{2}}.$ Tính độ dài đáy BC?

Bài 2: Cho hình bên, biết $ BM=8cm;$ $ MC=4cm;$ diện tích hình tam giác $ ABM=41,6c{{m}^{2}}.$ Tính diện tích hình tam giác ABC.

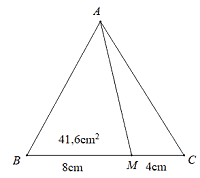
Các dạng bài tập Toán lớp 5 ôn hè lên 6

Bài 3: Một hình tam giác có cạnh đáy bằng $ \frac{7}{4}$ chiều cao. Nếu kéo dài cạnh đáy thêm 5m thì diện tích của tam giác đó tăng thêm $ 30{{m}^{2}}.$ Tính diện tích của hình tam giác đó.

Bài 4: Một thửa ruộng hình thang có diện tích $ 22,5{{m}^{2}}$ và chiều cao 5m. Tính:

a) Tổng hai đáy của thửa ruộng.

b) Đáy lớn và đáy bé của thửa ruộng biết rằng tỉ số của chúng là $ \frac{3}{2}.$

Bài 5: Một thửa ruộng hình thang có đáy lớn 150m, đáy bé bằng $ \frac{2}{3}$ đáy lớn. Đáy bé hơn chiều cao 15m. Trung bình cứ $ 100{{m}^{2}}$ thu hoạch được 74,5kg thóc. Tính số ki-lô-gam thóc thu hoạch được trên thửa ruộng đó?

Bài 6: Một mảnh vườn hình thang có độ dài đáy lớn 45m; đáy bé 35m và chiều cao bằng $ \frac{2}{5}$ tổng độ dài hai đáy. Người ta trồng rau trên mảnh vườn đó, trung bình cứ 3m2 thu hoạch được 9kg rau. Hỏi trên cả mảnh vườn người ta thu hoạch được bao nhiêu tấn rau?

Bài 7: Một thửa ruộng hình tứ giác ABCD có góc A và D vuông. Biết $ AB=60m,$ $ CD=80m,$ $ DA=40m.$ Người ta đắp một con đường theo cạnh CD rộng bằng $ \frac{1}{5}$ cạnh DC. Hỏi diện tích thửa đất còn lại là bao nhiêu, biết diện tích thửa đất lúc chưa đắp đường là $ 2800{{m}^{2}}.$

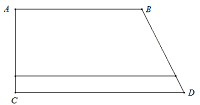
Các dạng bài tập Toán lớp 5 ôn hè lên 6-1

Bài 8: Một cái ao hình tròn có đường kính 18m. Tính diện tích của cái ao đó?

Bài 9: Hai ngày bạn An đi học bằng xe đạp, An nhận thấy cứ đạp được 15 vòng bánh xe thì đi được đoạn đường dài 28,26m. Hỏi đường kính của bánh xe mà bạn An đang đi dài bao nhiêu xăng-ti-mét?

2. Bài toán tính diện tích xung quanh, diện tích toàn phần

Bài 1: Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình lập phương

Cạnh4cm1,4dm0,5dm
Diện tích xung quanh
Diện tích toàn phần
Thể tích

Bài 2: Tính diện tích xung quanh, diện tích toàn phần và thể tích của hình hộp chữ nhật

Chiều dài4dm3,2m58,3cm
Chiều rộng3dm2,1m40cm
Chiều cao5dm1,5m35cm
Diện tích xung quanh
Diện tích toàn phần
Thể tích

Bài 3: Người ta làm một cái hộp không nắp bằng bìa cứng dạng hình lập phương cạnh 1,5dm. Hỏi diện tích bìa cần dùng để làm hộp bằng bao nhiêu đề-xi-mét vuông (không tính mép dán)?

Bài 4:

a) Hình lập phương thứ nhất có cạnh 8cm, hình lập phương thứ hai có cạnh 4cm. Tính diện tích xung quanh của mỗi hình lập phương.

b) Diện tích xung quanh của hình lập phương thứ nhất gấp mấy lần diện tích của hình lập phương thứ hai?

Bài 5: Một  cái hộp dạng hình hộp chữ nhật có chiều dài 20 cm, chiều rộng 15 cm và chiều cao 10cm. Bạn Bình dán giấy màu đỏ vào các mặt xung quanh và dán giấy màu vàng vào hai mặt đấy của hộp đó (chỉ dán mặt ngoài). Hỏi diện tích giấy màu nào lớn hơn và lớn hơn bao nhiêu xăng-ti-mét vuông?

3. Bài toán bể cá

Bài 1: Một bể nước hình hộp chữ nhật có chiều sai 4,5m, chiều rộng là 2,5m và chiều cao là 1,8m (không có nắp)

a) Tính diện tích xung quanh và diện tích toàn phần của bể nước đó

b) Bể đó chứa được nhiều nhất bao nhiêu lít nước ?

c) Trong bể đang có $ 16,2{{m}^{3}}$ nước. Tính chiều cao của mực nước trong bể?

Bài 2: Một bể nuôi cá hình hộp chữ nhật có chiều dài 1m, chiều rộng 50cm và chiều cao 60m.

a) Tính diện tích kính dùng làm bể cá đó (bể không có nắp)
b) Tính thể tích bể cá đó
c) Mực nước trong bể cao bằng $ \frac{3}{4}$ chiều cao của bể. Tính thể tích nước trong bể đó.

Bài 3: Một bể chứa nước hình hộp chữ nhật. Đo trong lòng bể: chiều dài 2,5m, chiều rộng 2,3m, chiều cao 1,6m. Hỏi bể chứa đầy nước thì được bao nhiêu lít? $ 1l=1d{{m}^{3}}.$

Bài 4: Một bể nước hình lập phương (không có nắp) có cạnh 0,6m

a) Tính diện tích toàn phần của bể nước

b) Trong bể đang chứa nước đến $ \frac{2}{3}$ bể. Hỏi phải đổ thêm mấy lít thì bể mới đầy? Biết $ 1l=1d{{m}^{3}}.$

Bài 5: Một bể cá hình hộp chữ nhật có chiều dài 0,5m, chiều rộng 0,3m. Trong bể chứa 48 lít nước. Mực nước trong bể bằng $ \frac{4}{5}$ chiều cao của bể. Hỏi chiều cao của bể là bao nhiêu mét?

Bài 6: Một bể cá hình hộp chữ nhật có chiều dài 80cm, chiều rộng 50cm và chiều cao 50cm. Cần đổ vào bể bao nhiêu lít nước để 80% thể tích của bể có nước?

Bài 7: Một bể cá hình hộp chữ nhật dài 1,6m, rộng 1,25m và cao 18dm. Người ta dùng thùng hình hộp chữ nhật dài 5dm, rộng 3dm, cao 4dm để đổ nước vào bể. Hỏi phải đổ vào bể bao nhiêu thùng nước như thế thì bể đầy nước?

4. Bài toán sơn phòng

Bài 1: Một phòng họp hình hộp chữ nhật có chiều dài 12m, chiều rộng 6m, chiều cao 4m. Người ta quét sơn mặt trong của phòng họp đó (bao gồm mặt trong của các bức tưởng và trần nhà). Hỏi diện tích cần quét sơn là bao nhiêu $ {{m}^{2}},$ biết rằng diện tích cửa ra vào và cửa số là $ 32{{m}^{2}}.$

Bài 2: Người ta lăn sơn tường bên trong một phòng học hình hộp chữ nhật có kích thước: dài 8m, rộng 6m, cao 4m. Phòng học có trần phẳng và 6 cửa sổ, mỗi cửa rộng 1,2m, cao 1,5m và một cửa ra vào rộng 1,2m, cao 2,2m. Tính diện tích cần lăn sơn.

Bài 3: Một người thợ nhận sơn tường của một căn phòng hình hộp chữ nhật có chiều dài 16m, chiều rộng 3m, chiều cao 4,8m. Biết sơn mỗi mét vuông tường người đó nhận đc 80.000 đồng tiền công và sơn mỗi mét vuông trần người đó nhận được 100.000 đồng tiền công. Sau khi sơn xong cả tường và trần của phòng thì người thợ nhận được bao nhiêu tiền?

Bài 4: Người ta quét sơn phía trong một phòng mái bằng có chiều dài 7,5m, chiều rộng 4,5m và chiều cao 3,5m. Biết phòng học có 1 cửa ra vào cao 2,2m, rộng 1,2m và 5 cửa sổ cao 1,2m, rộng 0,9m. Tính số tiền sơn để sơn phòng học đó. Biết giá 1kg sơn là 250000 và mỗi kg sơn chỉ sơn $ 15{{m}^{2}}.$

Bài 5: Người ta thuê sơn mặt trong và mặt ngoài của một cái thùng sắt không có nắp dạng hình lập phương cạnh 0,8m.

a) Tính diện tích cần phải sơn.

b) Giá tiền mỗi mét vuông là 15 000 đồng. Hỏi người đó phải trả bao nhiêu tiền?

VI. Toán chuyển động

1. Chuyển động cùng chiều

Bài 1: Quãng đường từ Hà Nội về thành phố H dài 150km. Lúc 7 giờ một ô tô đi từ Hà Nội về thành phố H với vận tốc 60km/giờ. Đến nơi, người lái xe nghỉ trả khách và ăn trưa mất 1 giờ 20 phút. Sau đó ô tô trở về Hà Nội với vận tốc 50km/giờ. Hỏi ô tô về đến Hà Nội lúc mấy giờ?

Bài 2: Một người đi xe máy khởi hành tại A lúc 5 giờ 15 phút với vận tốc 30km/giờ. Đến 7 giờ 15 phút một ô tô cũng bắt đầu đi từ A đuổi theo xe máy với vận tốc 45km/giờ. Hỏi ô tô đuổi kịp xe máy lúc mấy giờ?

Bài 3: Một ô tô và một xe máy cùng xuất phát lúc 7 giờ 30 phút để đi từ A đến B. Vận tốc của xe máy bằng $ \frac{3}{4}$ vận tốc của ô tô. Hỏi xe máy đến B lúc mấy giờ, biết quãng đường AB dài 120km và ô tô đến B lúc 10 giờ.

Bài 4: Ba xe ô tô cùng khởi hành lúc 7 giờ 30 phút sáng từ tỉnh A tới tỉnh B. Xe thứ 2 đi với vận tốc 45km/h và đã tới B lúc 11 giờ. Xe thứ 2 đã đến B sớm hơn xe thứ nhất là nửa giờ và đến muộn hơn xe thứ 3 cũng nửa giờ. Hỏi:

a) Xe thứ nhất và xe thứ 3 đã đến B khi nào?

b) Tính quãng đường từ tỉnh A tới tỉnh B dài bao nhiêu ki-lô-mét?

c) Vận tốc của xe thứ nhất và xe thứ ba là bao nhiêu ki-lô-mét?

Bài 5: Một xe máy đi từ A với vận tốc 40km/h, Xe máy đi được $ \frac{1}{2}$ giờ thì có một ô tô cũng đi từ A và đuổi theo xe máy. Hỏi sau bao lâu ô tô đuổi kịp xe máy. Biết vận tốc của ô tô là 55km/h.

Bài 6: Một người đi xe đạp khởi hành từ A với vận tốc 12,3km/giờ đuổi theo một người đi bộ khởi hành từ B. Hai người cùng khởi hành một lúc và sau 1 giờ 6 phút thì gặp nhau. Tính quãng đường AB biết rằng vận tốc người đi bộ bằng $ \frac{1}{3}$ vận tốc người đi xe đạp.

Bài 7: Anh Nam đi xe máy từ Hà Nội về quê. Nếu đi với vận tốc 30km/giờ thì về sớm 1 giờ so với quy định, còn nếu đi với vận tốc 20km/giờ thì lại đến nơi muộn hơn 1 giờ so với dự định. Hỏi:

a) Quãng đường từ Hà Nội về quê anh Nam dài bao nhiêu ki-lô-mét?

b) Anh Nam đi với vận tốc bao nhiêu km/giờ thì đến nơi đúng dự định?

2. Chuyển động ngược chiều

Bài 1: Một ô tô đi từ thị xã A đến thị xã B với vận tốc 48km/giờ. Cùng lúc đó một ô tô đi từ thị xã B đến thị xã A với vận tốc 54km/giờ. Sau 2 giờ hai ô tô gặp nhau. Tính quãng đường từ thị xã A đến thị xã B.

Bài 2: Một người đi từ A đến B với vận tốc 38,6km/giờ. Một người khác đi từ B đến A với vận tốc 44,8km/giờ. Quãng đường AB dài 208,5km. Hai người ra đi cùng một lúc. Hỏi sau bao lâu thì hai người gặp nhau.

Bài 3: Lúc 6 giờ một người xuất phát để đi từ A đến B với vận tốc 35km/giờ. Cùng lúc đó một người khác đi từ B về A với vận tốc 40km/giờ. Quãng đường AB dài 187,5km. Hỏi họ gặp nhau lúc mấy giờ?

Bài 4: Lúc 7 giờ một xe máy đi từ A và một xe đạp có vận tốc bằng $ \frac{2}{5}$ vận tốc của xe máy đi từ B ngược chiều nhau. Hai xe gặp nhau lúc 9 giờ 15 phút. Tính vận tốc mỗi xe biết quãng đường AB dài 94,5km.

Bài 5: A cách B 162km. Lúc 7 giờ 30 phút một xe máy có vận tốc 32,4km/h đi từ A về B. Sau đó 50 phút, một ô tô có vận tốc 48,6km/h khởi hành từ B đi về A. Hỏi

a) Hai xe gặp nhau lúc mấy giờ?

b) Chỗ gặp nhau cách A bao xa?

Bài 6: Cùng một lúc, một xe ô tô xuất phát từ A và một xe máy xuất phát từ B. Quãng đường AB dài 126km. Hai xe đi ngược chiều nhau và gặp nhau sau 1 giờ 30 phút.

a) Tính vận tốc của ô tô và vận tốc của xe máy? Biết mỗi giờ ô tô đi nhanh hơn xe máy 8km

b) Chỗ hai xe gặp nhau cách A bao nhiêu ki-lô-mét?

c) Nếu cùng xuất phát lúc 8 giờ 15 phút thì hai xe gặp nhau lúc mấy giờ?

VII. Nâng cao

Bài 1: Tính giá trị của biểu thức

$ A=\left( {6:\frac{3}{5}-1\frac{1}{6}\times \frac{6}{7}} \right):\left( {4\frac{1}{5}\times \frac{{10}}{{11}}+5\frac{2}{{11}}} \right)$

$ B=\left( {1-\frac{1}{2}} \right)\times \left( {1-\frac{1}{3}} \right)\times \left( {1-\frac{1}{4}} \right)\times …\times \left( {1-\frac{1}{{2017}}} \right)\times \left( {1-\frac{1}{{2018}}} \right)$

$ C=\frac{1}{{1\times 2}}+\frac{1}{{2\times 3}}+\frac{1}{{3\times 4}}+…+\frac{1}{{2017\times 2018}}$

$ D=\frac{1}{{1\times 4}}+\frac{1}{{4\times 7}}+\frac{1}{{7\times 10}}+…+\frac{1}{{97\times 100}}$

$ E=\frac{1}{{5\times 9}}+\frac{1}{{9\times 13}}+\frac{1}{{13\times 17}}+…+\frac{1}{{41\times 45}}$

$ F=\frac{{2005\times 2004-1}}{{2003\times 2005+2004}}$

$ G=\left( {1-\frac{1}{{1+2}}} \right)\times \left( {1-\frac{1}{{1+2+3}}} \right)\times \left( {1-\frac{1}{{1+2+3+4}}} \right)+…+\left( {1-\frac{1}{{1+2+3+…+2018}}} \right)$

$ H=\left( {1+\frac{7}{9}} \right)\times \left( {1+\frac{7}{{20}}} \right)\times \left( {1+\frac{7}{{63}}} \right)\times …\times \left( {1+\frac{7}{{2900}}} \right)$

Bài 2: Một hình hộp chữ nhật có số đo chiều rộng, chiều dài, chiều cao (đơn vị tính là dm) theo thứ tự đó là ba số đo tự nhiên liên tiếp tăng dần. Nếu giảm số đo chiều cao đi 2dm thì diện tích xung quanh của hình hộp chữ nhật mới bằng 60% diện tích xung quang của hình hộp chữ nhật ban đầu. Tính thể tích của hình hộp chữ nhật ban đầu.

Toán lớp 5 - Tags: