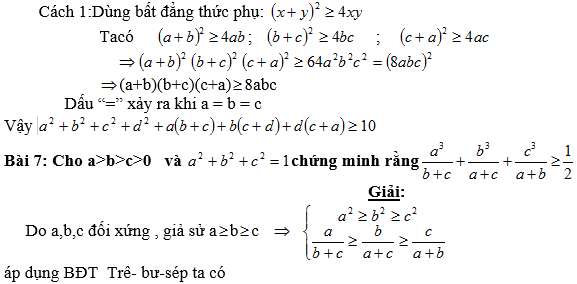Bất đẳng thức, tìm giá trị min-max của biểu thức
Bất đẳng thức là một dạng Toán khó trong chương trình Toán trung học cơ sở. Trong đó có dạng tìm giá trị min-max, còn gọi là tìm giá trị nhỏ nhất, lớn nhất.
Trong chuyên đề này, các em theo dõi những bài tập có lời giải, dưới mỗi bài tập sẽ có ghi ra hướng dẫn ghi nhớ các bất đẳng thức, cách tiếp cận bài toán tìm GTLN, GTNN.
Bài 1:
∀ x, y, z chứng minh rằng :
a) x2 + y2 + z2 ≥ xy+ yz + zx
b) x2 + y2 + z2 ≥ 2xy – 2xz + 2yz
c) x2 + y2 + z2 + 3 ≥ 2 (x + y + z)
Giải:
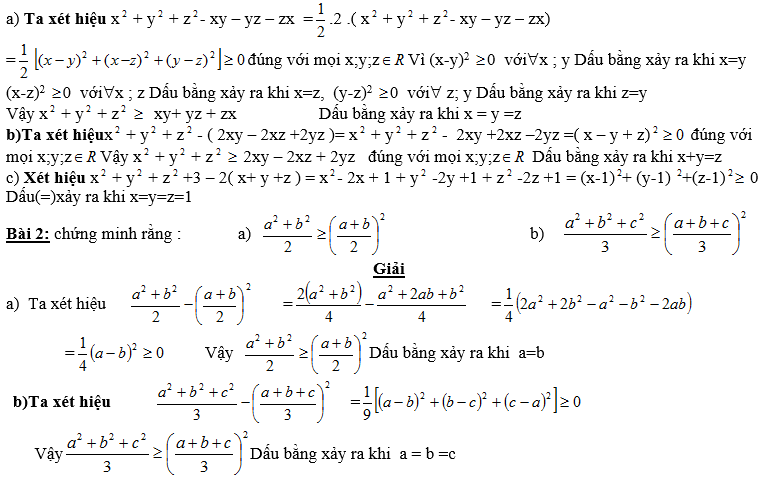
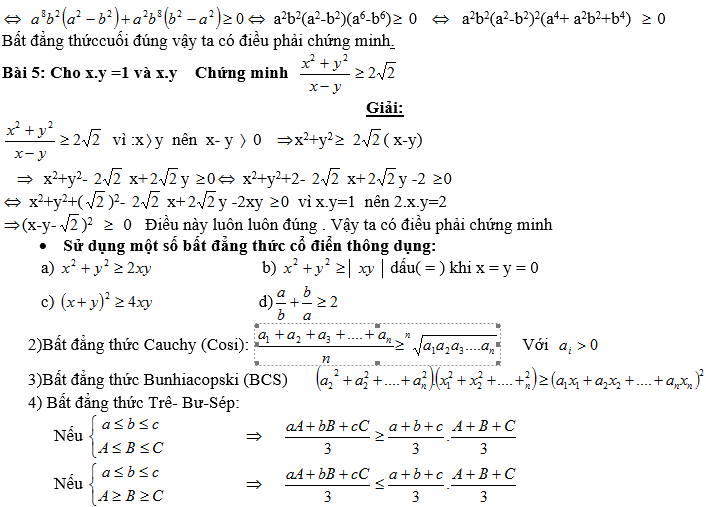
Dấu bằng xảy ra khi $ \displaystyle \left\{ \begin{array}{l}a=b=c\\A=B=C\end{array} \right.$
Bài 6: Cho a, b ,c là các số không âm chứng minh rằng:
(a+b)(b+c)(c+a) ≥ 8abc
Giải:
