9 sai lầm cơ bản trong giải toán trắc nghiệm

Trung tâm Gia sư Hà Nội đưa ra 9 sai lầm cơ bản trong giải toán trắc nghiệm mà học sinh thường mắc phải. Giúp các em đạt kết quả cao trong các bài thi trắc nghiệm Toán.

Những nhầm lẫn này được nêu ra kèm theo ví dụ thực tế giúp học sinh thấy rõ hơn, từ đó không mắc phải lỗi.

I. Nhầm lẫn các loại điều kiện

(điều kiện cần, điều kiện đủ, điều kiện cần và đủ)

1.1 Khi mệnh đề: $”A\Rightarrow B”$ (nếu có $A$ thì có $B$) đúng, học sinh có thể ngộ nhận về kết quả: Khẳng định $”B\Rightarrow A”$ (nếu có $B$ thì có $A$) đúng.

Ví dụ 1: Nếu hàm số $y=f\left(x\right)$ có đạo hàm tại $x=a$ thì hàm số liên tục tại $x=a$. Tuy nhiên, khẳng định sau là sai: Nếu hàm số $y=f\left(x\right)$ liên tục tại $x=a$ thì hàm số có đạo hàm tại $x=a$. Chẳng hạn, hàm số $y=|x-a|$ liên tục tại $x=a$ nhưng không có đạo hàm tại $x=a$.

Ví dụ 2: Nếu hàm số $y=f\left(x\right)$ có đạo hàm tại điểm $x=x_0$ và đạt cực trị tại điểm đó thì $f^{\prime }\left(x_0\right)=0$. Tuy nhiên, khẳng định sau là sai: Nếu hàm số $y=f\left(x\right)$ có đạo hàm tại điểm $x=x_0$ và $f^{\prime }\left(x_0\right)=0$ thì hàm số đạt cực trị tại điểm $x=x_0$. Chẳng hạn, hàm số $f\left(x\right)=x^3+1$ có đạo hàm tại $x=0$ và $f^{\prime }\left(0\right)=0$ nhưng không đạt cực trị tại điểm $x=0$.

Ví dụ 3: Hàm số $f\left(x\right)=x^4-6x^2+8x+1$ có bao nhiêu điểm cực trị?

A. 0;                     B. 1;                     C. 2;                     D. 3;

Trong ví dụ này học sinh dễ sai lầm lựa chọn đáp án C do khi tính đạo hàm của hàm số đã cho $f^{\prime }\left(x\right)=4x^3-12x+8$ có hai nghiệm là $x=1$ và $x=-2$. Tuy nhiên ở đây, tại $x=1$ là nghiệm kép, đạo hàm $f^{\prime }\left(x\right)$ không đổi dấu khi đi qua $x=1$ nên hàm số không đạt cực trị tại điểm này. Phương án đúng là B.

1.2 Khi mệnh đề: $”A\Rightarrow B”$ (nếu có $A$ thì có $B$)  đúng, học sinh có thể bị ngộ nhận về kết quả: Khẳng định $”\bar{A}\Rightarrow \bar{B}”$ (nếu không có$A$ thì không có $B$) đúng.

Ví dụ 4: Nếu hàm số $y=f\left(x\right)$ có đạo hàm tại $x=a$ thì hàm số liên tục tại $x=a$. Tuy nhiên, khẳng định sau là sai: Nếu hàm số $y=f\left(x\right)$ không có đạo hàm tại $x=a$ thì hàm số không liên tục tại $x=a$. Chẳng hạn, hàm số $y=|x-a|$ không có đạo hàm tại $x=a$ nhưng vẫn liên tục tại $x=a$.

1.3 Khi mệnh đề: $”A\Rightarrow B”$ (nếu có $A$ thì có $B$)  đúng, học sinh có thể bị ngộ nhận về kết quả: Khẳng định $”\bar{A}\Rightarrow B”$ (nếu không có$A$ thì có $B$) sai.

Ví dụ 5: Nếu $z$ là số thực thì môđun của $z$ là một số không âm. Khẳng định sau vẫn đúng: Nếu $z$ không là số thực thì môđun của $z$ là một số không âm.

II. Nhầm lẫn giữa giả thiết trong câu hỏi trắc nghiệm và giả thiết của các định lí trong sách giáo khoa

Ví dụ 6: Xét các khẳng định sau:

i) Nếu hàm số $y=f\left(x\right)$ xác định trên $\mathbb{R}$ thỏa mãn $f(-1).f\left(0\right)<0$ thì đồ thị của hàm số $y=f\left(x\right)$ và trục hoành có ít nhất 1 điểm chung.

ii) Nếu hàm số $y=f\left(x\right)$ xác định trên $\mathbb{R}$ thỏa mãn $f(-1).f\left(0\right)<0$ và $f\left(0\right).f\left(1\right)<0$ thì đồ thị của hàm số $y=f\left(x\right)$ và trục hoành có ít nhất 2 điểm chung.

Phát biểu nào sau đây đúng?

A. Khẳng định i) đúng và khẳng đinh ii) đúng;

B. Khẳng định i) đúng và khẳng định ii) sai;

C. Khẳng định i) sai và khẳng định ii) đúng;

D. Khẳng định i) sai và khẳng định ii) sai;

Đây là một câu hỏi khó, học sinh có thể liên tưởng đến định lí về giá trị trung gian của hàm số liên tục khi đọc các giả thiết ở hai khẳng định này. Tuy nhiên, các giả thiết thiếu một điều kiện rất quan trọng là hàm số liên tục. Ta có thể chỉ ra những tình huống để thấy các khẳng định i) và ii) đều sai.

Xét hàm số $f\left(x\right)=\{\begin{array}{l}-1khix\in \mathbb{R}\mathrm{\setminus }\left\{0\right\}\\ 1khix=0\end{array}$. Hàm số này không liên tục tại $x=0$.

Ta có $f(-1).f\left(0\right)<0,f\left(0\right).f\left(1\right)<0$ và đồ thị của hàm số không có điểm chung với $Ox$. Chọn phương án D.

Ví dụ 7: Điểm cực tiểu của đồ thị hàm số $y=-x^3+3x+4$ là:

A. $x_{CT}=-1$;                               B. $x_{CT}=1$;

C. $(-1;2)$;                            D. $(1;6)$;

Trong ví dụ này học sinh dễ nhầm lẫn giữa phương án A và phương án C. Nếu hàm số $f\left(x\right)$ đạt cực tiểu tại $x_0$ thì $x_0$ được gọi là điểm cực tiểu của hàm số; $f\left(x_0\right)$ được gọi là giá trị cực tiểu của hàm số, còn điểm $M(x_0;f\left(x_0\right))$ được gọi là điểm cực tiểu của đồ thị hàm số. Bởi vậy phương án đúng phải là C.

Ví dụ 8: Cho hàm số $y=f\left(x\right)$ xác định trên $\mathbb{R}\mathrm{\setminus }\{1;3\}$ và có $\underset{x\to +\mathrm{\infty }}{lim}y=2$, $\underset{x\to 3^{+}}{lim}y=-\mathrm{\infty }$, $\underset{x\to 1^{-}}{lim}y=+\mathrm{\infty }$. Khẳng định nào sau đây là sai?

A. Đồ thị hàm số có ít nhất một tiệm cận ngang là đường thẳng $y=2$ và hai tiệm cận đứng là đường thẳng $x=1$ và $x=3$;

B. Đường thẳng $x=1$ là một tiệm cận đứng của đồ thị hàm số;

C. Đường thẳng $x=3$ là một tiệm cận đúng của đồ thị hàm số;

D. Hàm số có hai tiệm cận đứng là $x=1$ và $x=3$;

Trong ví dụ này học sinh sẽ gặp khó khăn trong việc lựa chọn phương án đúng do khi đọc 4 phương án sẽ có cảm giác cả 4 khẳng định đều đúng. Trong sách giáo khoa đưa ra định nghĩa về tiệm cận đứng (tiệm cận ngang) đều nêu rõ là của đồ thị hàm số. Ở đây phương án D thiếu dữ kiện là đồ thị hàm số. Chọn phương án D.

III. Xét thiếu trường hợp trong quá trình tìm ra kết quả cuối cùng

Ví dụ 9: Tìm $m$ để hàm số $y=m{x}^3+m{x}^2+(2m+1)x-1$ đồng biến trên tập xác định.

Học sinh cần chú ý xét riêng trường hợp $m=0$ trước khi dùng định lí về dấu của tam thức bậc hai. Trong tình huống này, $m=0$ thỏa mãn yêu cầu bài toán. Với hàm số trên, người ta có thể xây dựng 1 phương án nhiễu là thiếu số 0 trong tập hợp các kết quả.

Ví dụ 10: Tập hợp các số thực $m$ đề hàm số $y=\frac{m{x}^3}{3}-(m+1)x^2+4x-1$ có cực trị là:

A. $\mathbb{R}\mathrm{\setminus }\left\{1\right\}$;                          B. $\mathbb{R}$;

C. $\mathbb{R}\mathrm{\setminus }\{0;1\}$;                       D. $\mathbb{R}\mathrm{\setminus }\left\{0\right\}$;

Trong ví dụ này học sinh dễ quên trường hợp $m=0$, hàm số bậc hai luôn có cực trị, vì vậy $m=0$ thuộc tập hợp các kết quả. Phương án đúng là A.

Ví dụ 11: Trong không gian $Oxyz$, cho hai điểm $B(0;2;0)$ và $C(0;0;2)$. Phương trình mặt phẳng $\left(P\right)$ chứa $BC$ và cách điểm $M(1;2;-1)$ một khoảng bằng $\frac{1}{\sqrt{2}}$ là:

A. $y+z-2=0$;

B. $2x+\frac{1}{2}y+\frac{1}{2}z-1=0$;

C. $2x-\frac{1}{2}y-\frac{1}{2}z+1=0$ hoặc $y-z+2=0$;

D. $2x+\frac{1}{2}y+\frac{1}{2}z-1=0$ hoặc $y+z-2=0$;

Trong ví dụ này học sinh thường có hướng giải theo phương trình mặt phẳng theo đoạn chắn. Gọi giao điểm của mặt phẳng $\left(P\right)$ với trục $Ox$ là điểm $A(a;0;0)$. Phương trình mặt phẳng $\left(P\right)$ có dạng: $\frac{x}{a}+\frac{y}{2}+\frac{z}{2}=1\iff 2x+ay+az-2a=0$.

Theo giả thiết: $d(M;\left(P\right))=\frac{|2-a|}{\sqrt{4+2a^2}}=\frac{1}{\sqrt{2}}\iff a=\frac{1}{2}$.

Phương trình mặt phẳng $\left(P\right)$ là: $2x+\frac{1}{2}y+\frac{1}{2}z-1=0$.

Khi giải đến đây học sinh dễ mắc sai lầm lựa chọn phương án B mà quên mất một trường hợp nữa là mặt phẳng $\left(P\right)$ có thể không được viết dưới dạng phương trình của mặt phẳng theo đoạn chắn. Ở đây học sinh cần phải xét thêm một trường hợp nữa là $\left(P\right)\Vert Ox$. Khi đó, vectơ pháp tuyến của mặt phẳng $\left(P\right)$ được tính: $\overrightarrow{n}=[\overrightarrow{AB},\overrightarrow{i}]=(0;2;2)$. Ta lập được phương trình mặt phẳng $\left(P\right)$ theo trường hợp này là: $y+z-2=0$. Trường hợp này thỏa mãn yêu cầu bài toán nên phương án đúng là D.

Ví dụ 12: Cho hàm số $y=-\frac{1}{3}{x}^3+(m-m^2-2)x^2-(3m^2+1)x-m$. Tìm $m$ để hàm số đạt cực trị tại điểm $x=-2$.

A. $m=1$;                                       B. $m=1$ hoặc $m=3$;

C. $m=3$;                                       D. Đáp án khác;

Trong ví dụ này học sinh dễ nhầm lẫn giữa phương án B và phương án C.

Đạo hàm của hàm số: $y^{\prime }=-x^2+2(m-m^2-2)x-(3m^2+1)$.

Điều kiện cần để hàm số đạt cực trị tại $x=-2$ là $y^{\prime }(-2)=0$

$\begin{array}{l}\iff -4-4(m-m^2-2)-(3m^2+1)=0\\ \iff [\begin{array}{c}m=1\\ m=3\end{array}\end{array}$

Khi giải đến đây hàm số vội vàng lựa chọn phương án B mà quên mất việc xét điều kiện đủ để hàm số đạt cực trị tại $x=-2$.

Điều kiện đủ: +, Với $m=1$ thì $y^{\prime }=-x^2-4x-4=-{(x+2)}^3\le 0,\mathrm{\forall }x\in \mathbb{R}$. Bởi vậy hàm số nghịch biến trên $\mathbb{R}$ nên không có cực trị.

+, Với ${\displaystyle m=3}$ thì $y^{\prime }=-x^2-16x-28$ và $y”=-2x-16$.

Khi đó $\begin{array}{l}{y}^{\prime }(-2)=0\\ y”(-2)=-12<0\end{array}\}\Rightarrow$ hàm số đạt cực đại tại $x=-2$.

Vậy $m=3$ thì hàm số đạt cực trị tại $x=-2$. Chọn phương án C.

IV. Ngộ nhận về kết quả tổng quát khi mới biết một số trường hợp riêng

Ví dụ 13: Số đường tiệm cận đứng của đồ thị hàm số $y=\frac{1}{x^2-3x+2}$ là:

A. $\mathbb{R}\mathrm{\setminus }\left\{1\right\}$;                  B. $\mathbb{R}$;

C. $\mathbb{R}\mathrm{\setminus }\{0;1\}$;               D. $\mathbb{R}\mathrm{\setminus }\left\{0\right\}$;

Khi nhìn mẫu số có 2 nghiệm là 1 và 2, học sinh có thể đưa ra đúng đáp án cho câu hỏi này là đáp án C. Trong tình huống này, phương án C là phương án đúng vì: $\underset{x\to 1^{-}}{lim}\frac{1}{x^2-3x+2}=+\mathrm{\infty },\underset{x\to 2^{+}}{lim}\frac{1}{x^2-3x+2}=+\mathrm{\infty },\underset{x\to a}{lim}\frac{1}{a^2-3a+2}\mathrm{\forall }a\notin \{1;2\}$ .

Tuy nhiên số tiệm cận đứng của đồ thị không phải lúc nào cũng bằng số nghiệm phân biệt của mẫu số. Chẳng hạn câu hỏi sau:

Số đường tiệm cận của đứng của đồ thịhàm số $y=\frac{(\sqrt{x+3}-2)}{x^2-x}$ là:

A. 3;                        B. 2;                     C. 0;                      D. 1;

Mẫu số có hai nghiệm phân biệt là 0 và 1 nhưng đồ thị không có tiệm cận đứng vì:

$\underset{x\to 0}{lim}\frac{(\sqrt{x+3}-2)}{x^2-x}=\underset{x\to 0}{lim}\frac{\sin x}{x}.\frac{\sqrt{x+3}-2}{x-1}=2-\sqrt{3}$ khác vô cực.

$\underset{x\to 1}{lim}\frac{(\sqrt{x+3}-2)}{x^2-x}=\underset{x\to 1}{lim}\frac{(x+3-2^2)\sin x}{(\sqrt{x+3}+2)(x-1)x}=\frac{\sin 1}{4}$ khác vô cực.

Chọn phương án C.

Ví dụ 14: Xét các mệnh đề sau:

1. Đồ thị hàm số $y=\frac{1}{2x+1}$ có một tiệm cận đứng và một tiệm cận ngang.

2. Đồ thị hàm số $y=\frac{x+\sqrt{x^2+x+1}}{x}$ có hai tiệm cận ngang và một tiệm cận đứng.

3. Đồ thị hàm số $y=\frac{x-\sqrt{2x-1}}{x^2-1}$ có một tiệm cận ngang và hai tiệm cận đứng.

Số mệnh đề đúng là:

A. 1;                         B. 2;                     C. 3;                     D. 0;

Học sinh dễ dàng kiểm tra nhanh mệnh đề 1 và mệnh đề 2 đúng. Trong ví dụ này học sinh dễ mắc sai lầm trong mệnh đề 3. Học sinh dễ dàng tìm ra đồ thị hàm số $y=\frac{x-\sqrt{2x-1}}{x^2-1}$ có một tiệm cận ngang là đường $y=0$ và ngộ nhận đồ thị hàm số có hai đường tiệm cận đứng là $x=-1$ và $x=1$. Lí do sai nhầm ở đây cũng giống trong ví dụ trên, mẫu số có hai nghiệm phân biệt là $-1$ và $1$ nhưng đồ thị không có đường tiệm cận đứng là $x=-1$ không tồn tại giới hạn khi $x\to -1^{+}$ hoặc $x\to -1^{-}$. Mệnh đề 3 sai. Chọn phương án B.

Ví dụ 15: Nếu $a$ và $b$ là hai số thực thì $\left|a\right|=\left|b\right|\iff [\begin{array}{l}a=b\\ a=-b\end{array}$.

Khẳng định sau đây là sai: Nếu $a$ và $b$ là hai số phức thì $\left|a\right|=\left|b\right|\iff [\begin{array}{l}a=b\\ a=-b\end{array}$

V. Ngộ nhận về tập hợp các kết quả trong khi chỉ mò được một số kết quả

Ví dụ 16: Số nghiệm thực của phương trình $3^x=x+2$ là:

A. 0;                      B. 1;                     C. 2;                     D. 3;

Trong ví dụ này học sinh mò được một nghiệm là 1 nhưng không mò được thêm nghiệm khác và có thể ngộ nhận số nghiệm của phương trình là 1.

Học sinh có thể vẽ đồ thị của các hàm số để thấy số nghiệm của phương trình là 2.

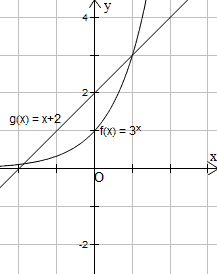
Ngoài ra, học sinh có thể xét hàm số liên tục trên $\mathbb{R}$, ${\displaystyle h\left(x\right)=3^x-x-2,h\left(1\right)=0,h(-2)>0,h(-1)<0}$, tồn tại $c\in (-2;-1),h\left(c\right)=0$.

$h”\left(x\right)=3^x{(\ln 3)}^2>0,\mathrm{\forall }x\in \mathbb{R}$ nên phương trình $h\left(x\right)=0$ có tối đa 2 nghiệm. Chọn phương án C.

Học sinh cũng có thể sử dụng một số loại máy tính để tìm ra số nghiệm của phương trình này.

VI. Quên điều kiện dẫn đến thừa kết quả trong bài toán

Ví dụ 17: Số nghiệm thực của phương trình $\frac{{\log }_2(x^2+3x)-2}{{\log }_{2}x}=0$ là:

A. 0;                       B. 1;                     C. 2;                     D. 3;

Nếu học sinh chỉ chú ý đến điều kiện $x>0$ và giải phương trình ${\log }_2(x^2+3x)-2=0$, có 2 kết quả là $x=-4$ (không thỏa mãn $x>0$) và $x=1$ thì chọn phương án B. Tuy nhiên, $x=1$ không thỏa mãn điều kiện mẫu số khác 0. Vì vậy phải chọn phương án A.

VII. Đưa ra điều kiện mới dẫn đến giảm số kết quả trong bài toán

Ví dụ 18: Số nghiệm thực của phương trình $2{\log }_2(3x+2)={\log }_2{x}^2$ là:

A. 0;                      B. 1;                     C. 2;                     D. 3;

Vì có hệ số 2 ở vế trái nên học sinh có thể nghĩ ngay đến công thức ${\log }_2{x}^2=2{\log }_{2}x$ khi $x$ dương, học sinh biến đổi về $3x+2=x\iff x=-1$. Giá trị này không thỏa mãn điều kiện để có thể thực hiện được công thức ${\log }_2{x}^2=2{\log }_{2}x$, học sinh có thể kết luận phương trình đã cho vô nghiệm.

Sai lầm ở đây là học sinh đưa ra điều kiện mới $x>0$ để biến đổi và làm mất nghiệm. Lời giải đúng như sau:

$2{\log }_2(3x+2)={\log }_2{x}^2\iff \{\begin{array}{l}3x+2>0\\ x^2>0\\ {\log }_2{(3x+2)}^2>{\log }_2{x}^2\end{array}$

$\iff \{\begin{array}{l}x>-\frac{2}{3}\\ x\ne 0\\ {(3x+2)}^2=x^2\end{array}\iff \{\begin{array}{l}x>-\frac{2}{3}\\ x\ne 0\\ 8x^2+12x+4=0\end{array}\iff x=-\frac{1}{2}.$

Chọn phương án B. Học sinh cần phải cảnh giác với những biến đổi dẫn đến phương trình mới có tập xác định khác với tập xác định ban đầu.

VIII. Sai lầm khách quan do lỗi máy tính điện tử

Ví dụ 19: Tính diện tích hình phẳng $S$ giới hạn bởi đồ thị hàm số $y=x^2-3x$ và hai đường thẳng $x=-15,x=15$.

A. $S=2250$;        B. $S=2259$;        C. $S=1593$;          D. $S=2925$;

Trong ví dụ này học sinh có lời giải đúng như sau:

Diện tích hình phẳng cần tính: $S=\underset{-15}{\overset{15}{\int }}|x^2-3x|dx=\underset{-15}{\overset{0}{\int }}(x^2-3x)dx-\underset{0}{\overset{3}{\int }}(x^2-3x)dx+\underset{3}{\overset{15}{\int }}(x^2-3x)dx=2259$. Chọn phương án B. Tuy nhiên đối với dạng bài tập kiểu này học sinh thường sẽ sử dụng máy tính điện tử để tính $S=\underset{-15}{\overset{15}{\int }}|x^2-3x|dx$. Khi dùng máy tính điện tử sẽ có hai khả năng sau:

• VINACAL: Ta tính $S=\underset{-15}{\overset{15}{\int }}|x^2-3x|dx=2259$. Đúng với kết quả tính tay.
• CASIO: Ta tính $S=\underset{-15}{\overset{15}{\int }}|x^2-3x|dx=2250$. Không đúng với kết quả tính tay.

Lý do nào hai loại máy tính này cho ta hai kết quả khác nhau là bởi vì: Máy CASIO “thường không đúng” cho tích phân trị tuyệt đối với hai cận chứa 3 đoạn đổi dấu trở nên.

Ví dụ 20: Tính diện tích hình phẳng $S$ giới hạn bởi đồ thị hàm số $y=x^2-x$ và hai đường thẳng $x=-12,x=12$.

A. $S=1152$;         B. $S=\frac{3457}{2}$;       C. $S=\frac{3457}{3}$;       D. $S=1154$;

Trong ví dụ này học sinh có lời giải đúng như sau:

Diện tích hình phẳng cần tính: $S=\underset{-12}{\overset{12}{\int }}|x^2-x|dx=\underset{-12}{\overset{0}{\int }}(x^2-x)dx-\underset{0}{\overset{1}{\int }}(x^2-x)dx+\underset{1}{\overset{12}{\int }}(x^2-x)dx=\frac{3457}{3}$. Chọn phương án C. Tuy nhiên đối với dạng bài tập kiểu này học sinh thường sẽ sử dụng máy tính điện tử để tính $S=\underset{-12}{\overset{12}{\int }}|x^2-x|dx$. Đối với ví dụ này thì cả hai loại máy CASIO và VINACAL đều cho ra cùng một đáp số là $1152$. Kết quả này chỉ là kết quả gần đúng. Khi đó học sinh dễ chọn phương án sai lầm là phương án A.

IX. Biến đổi sai biểu thức, tính toán sai

Học sinh phải thận trọng khi biến đổi biểu thức. Tránh tình trạng quá tin tưởng vào máy tính khi xử lí một biểu thức đã biến đổi sai và yên tâm dùng kết quả được tìm nhờ máy tính.

• Cách hạn chế sai lầm trong giải toán trắc nghiệm

• Bộ câu hỏi trắc nghiệm lý thuyết Toán 11 + 12 có đáp án

• Cách tra cứu điểm thi vào lớp 10 cả nước năm 2018

• Giáo án ôn tập Toán hè lớp 5 lên lớp 6 năm 2018

• Tài liệu bồi dưỡng HSG bất đẳng thức

• Các dạng toán về viết phương trình đường tròn

• Cách chứng minh 3 điểm thẳng hàng bằng vectơ